The Sine Calculator is a very useful online tool for calculating the sine value of a given degree or radian. All you have to do is enter degrees or radians into the calculator’s input box. No professional knowledge is required, and laymen can easily handle it.
What is sine?
Sine, one of the most commonly used trigonometric functions. In a right triangle, the sine of the acute angle is equal to the ratio of the length of the opposite side to the length of the hypotenuse. It is abbreviated as sin and is formulated as
sin(θ) = oppositehypotenuse
For example, there is a right triangle as follows
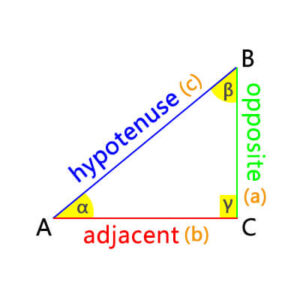 In this right triangle, the three angles are α, β and γ, where γ is the right angle. The three sides are a, b, and c, where c is the hypotenuse. Therefore, the sines of the three angles are
In this right triangle, the three angles are α, β and γ, where γ is the right angle. The three sides are a, b, and c, where c is the hypotenuse. Therefore, the sines of the three angles are
sin(α) = oppositehypotenuse = ac
sin(β) = adjacenthypotenuse = bc
sin(γ) = hypotenusehypotenuse = cc = 1
We know that in a right triangle, the hypotenuse is the longest, so the sine value must not be greater than 1. In fact, the sine ranges from -1 to 1.
How to calculate sine?
From the sine formula above, to calculate the sine value, we need to know the lengths of the opposite and hypotenuse.
For example, in a right-angled triangle, the length of the opposite side of angle α is 3, and the length of the adjacent side is 4 (as shown in the figure below), so what is the sine of angle α?
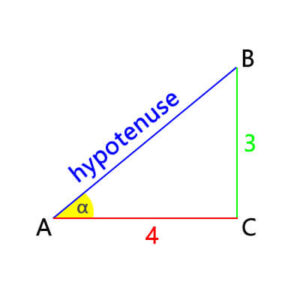 First, we need to calculate the length of the hypotenuse, according to the Pythagorean theorem
First, we need to calculate the length of the hypotenuse, according to the Pythagorean theorem
Hypotenuse2 = opposite2 + adjacent2
Therefore, the length of the hypotenuse is
Hypotenuse2 = opposite2 + adjacent2 = 32 + 42 = 25
Hypotenuse = 5
The hypotenuse length is 5. So, the sine of the angle α is
sin(α) = oppositehypotenuse = 35
Of course, this is calculated according to the definition of sine. If the lengths of the sides are not given, but the degree or radian of the angle is known, then you can use the sine calculator we provided above to calculate it directly or refer to the sine table to find the corresponding sine value. The sine table is as follows, including angles and radians.
| Degrees | Radians | Sine |
| 0° | 0 | 0 |
| 5° | π36 | 0.08715574 |
| 10° | π18 | 0.17364818 |
| 15° | π12 | 0.25881905 |
| 20° | π9 | 0.34202014 |
| 25° | 5π36 | 0.42261826 |
| 30° | π6 | 0.5 |
| 35° | 7π36 | 0.57357644 |
| 40° | 2π9 | 0.64278761 |
| 45° | π4 | 0.70710678 |
| 50° | 5π18 | 0.76604444 |
| 55° | 11π36 | 0.81915204 |
| 60° | π3 | 0.8660254 |
| 65° | 13π36 | 0.90630779 |
| 70° | 7π18 | 0.93969262 |
| 75° | 5π12 | 0.96592583 |
| 80° | 4π9 | 0.98480775 |
| 85° | 17π36 | 0.9961947 |
| 90° | π2 | 1 |
| 95° | 19π36 | 0.9961947 |
| 100° | 5π9 | 0.98480775 |
| 105° | 7π12 | 0.96592583 |
| 110° | 11π18 | 0.93969262 |
| 115° | 23π36 | 0.90630779 |
| 120° | 2π3 | 0.8660254 |
| 125° | 25π36 | 0.81915204 |
| 130° | 13π18 | 0.76604444 |
| 135° | 3π4 | 0.70710678 |
| 140° | 7π9 | 0.64278761 |
| 145° | 29π36 | 0.57357644 |
| 150° | 5π6 | 0.5 |
| 155° | 31π36 | 0.42261826 |
| 160° | 8π9 | 0.34202014 |
| 165° | 11π12 | 0.25881905 |
| 170° | 17π18 | 0.17364818 |
| 175° | 35π36 | 0.08715574 |
| 180° | π | 0 |
| 185° | 37π36 | -0.08715574 |
| 190° | 19π18 | -0.17364818 |
| 195° | 13π12 | -0.25881905 |
| 200° | 10π9 | -0.34202014 |
| 205° | 41π36 | -0.42261826 |
| 210° | 7π6 | -0.5 |
| 215° | 43π36 | -0.57357644 |
| 220° | 11π9 | -0.64278761 |
| 225° | 5π4 | -0.70710678 |
| 230° | 23π18 | -0.76604444 |
| 235° | 47π36 | -0.81915204 |
| 240° | 4π3 | -0.8660254 |
| 245° | 49π36 | -0.90630779 |
| 250° | 25π18 | -0.93969262 |
| 255° | 17π12 | -0.96592583 |
| 260° | 13π9 | -0.98480775 |
| 265° | 53π36 | -0.9961947 |
| 270° | 3π2 | -1 |
| 275° | 55π36 | -0.9961947 |
| 280° | 14π9 | -0.98480775 |
| 285° | 19π12 | -0.96592583 |
| 290° | 29π18 | -0.93969262 |
| 295° | 59π36 | -0.90630779 |
| 300° | 5π3 | -0.8660254 |
| 305° | 61π36 | -0.81915204 |
| 310° | 31π18 | -0.76604444 |
| 315° | 7π4 | -0.70710678 |
| 320° | 16π9 | -0.64278761 |
| 325° | 65π36 | -0.57357644 |
| 330° | 11π6 | -0.5 |
| 335° | 67π36 | -0.42261826 |
| 340° | 17π9 | -0.34202014 |
| 345° | 23π12 | -0.25881905 |
| 350° | 35π18 | -0.17364818 |
| 355° | 71π36 | -0.08715574 |
| 360° | 2π | 0 |
Sine graph and range
We all know that the sine function can be represented by a curve. This curve extends infinitely and fluctuates periodically. Now, draw part of the graph of the sine below.
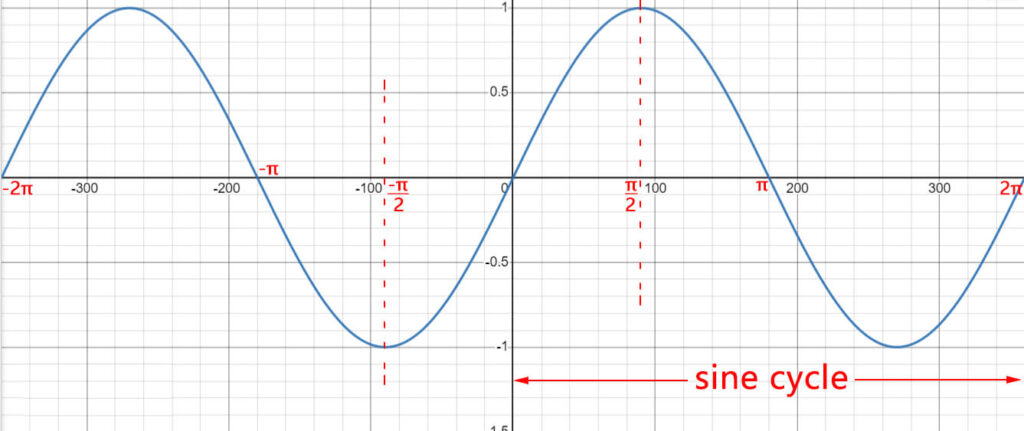 It can be seen that this curve fluctuates between -1 and 1, that is, the range of the sine value is between -1 and 1. At the same time, the curve repeats every 360 degrees, which also means that the period of the sine function is 360 degrees, that is, 2π radians. Expressed by the equation is
It can be seen that this curve fluctuates between -1 and 1, that is, the range of the sine value is between -1 and 1. At the same time, the curve repeats every 360 degrees, which also means that the period of the sine function is 360 degrees, that is, 2π radians. Expressed by the equation is
sin(θ) = sin(θ + n * 360°)
Here, n is an integer.
Also, you can observe that the sine curve is an axisymmetric figure. Take π/2 +kπ (k is an integer) as the axis of symmetry. The positive and negative values of sine are also obvious. It depends on which quadrant of the axis the sine function is in.
| Quadrant | Degrees | Radians | Sign | Sin Values | Monotonicity |
| 1 | 0° < θ < 90° | 0 < θ < π2 | + | 0 < sin(θ) < 1 | Ascending |
| 2 | 90° < θ < 180° | π2 < θ < π | + | 0 < sin(θ) < 1 | Decreasing |
| 3 | 180° < θ < 270° | π < θ < 3π2 | – | -1 < sin(θ) < 0 | Decreasing |
| 4 | 270° < θ < 360° | 3π2 < θ < 2π | – | -1 < sin(θ) < 0 | Ascending |
Other calculations for sine
There are 3 calculations closely related to sine.
1. Sine derivative
The derivative of the sine function is the cosine function (shorted as cos), so the derivative of the sine is equal to the ratio of the length of the adjacent side to the length of the hypotenuse.
sin'(θ) = cos(θ) = adjacenthypotenuse
2. Inverse sine
The inverse sine is also known as arcsine, which is used to find the angle from the sine value. It can be represented by sin-1. In the computer field, it is usually expressed as asin or asn.
sin(90°) = 1
sin-1(1) = arcsin(1) = 90°
3. Reciprocal sine
According to the definition of sine, it can be concluded that the reciprocal of the sine is equal to the ratio of the hypotenuse to the opposite side. That is, the cosecant in trigonometric functions, abbreviated as csc.
1sin(θ) = csc(θ)
How to use this sine calculator
This sine calculator is easy to use. First, choose the type, degrees or radians. Then, enter a value. Finally, click the Calculate button. The moment the button is released, the sine result appears immediately. Of course, if you want to perform a new sine calculation, please click the Reset button first.
FAQS
- Q: How to enter degrees? Would you like to enter the degree symbol?A: Enter the number directly without the degree symbol.
- Q: How to enter radians? What about pi?A: As with degrees, enter the numbers directly. If there is π, type or copy π and paste it. If not, please enter pi instead.
- Q: Can I enter a fraction? How to enter?A: Yes, sure. The numerator and denominator are divided by /, such as 1/2, 3π/4 and so on.
- Q: Why is sin 90° equal to 1?A: Because the opposite side of a right angle is also the hypotenuse, their ratio is 1. Therefore, the sine 90° is equal to 1.
- Q: What is the value of sin pi?A: pi stands for π, equal to 180 degrees. The sin of 180 degrees is 0. So, the sin of pi is 0.
Conclusion
In summary, the sine function is a very important function. It is the basis of trigonometry functions. So, it is very necessary to learn how to calculate sine and the related information of sine. In this article, we made a very comprehensive summary. At the same time, we also provide a sine calculator based on angles or radians, which allows you to quickly calculate the sine value. These will definitely benefit you a lot, don’t you think?
Latest Calculators
Standard Form to Slope-Intercept Form Calculator
Slope Intercept Form Calculator
Slope Calculator: Calculate Slope, X-Intercept, Y-Intercept
Reciprocal of Complex Number Calculator
Conjugate Complex Number Calculator
Modulus of Complex Number Calculator
Profit Percentage Calculator: Calculate Your Profitability Easily
Attendance and Absence Percentage Calculator
Trigonometric Functions
Arccsc Calculator – Find the Exact Value of Inverse Cosecant
Arcsec Calculator – Find the Exact Value of Inverse Secant
Arccot Calculator – Find the Exact Value of Inverse Cotangent
Arctan Calculator – Find the Exact Value of Inverse Tangent
Inverse Cosine Calculator – Find The Exact Value of Arccos
Inverse Sine Calculator – Find The Exact Value of Arcsin
Inverse Trigonometric Functions Calculator
Trigonometric Functions Conversion Calculator
Trig Calculator – Find 6 Trigonometric Functions by Angles or Sides