扇形计算器

什么是扇形？

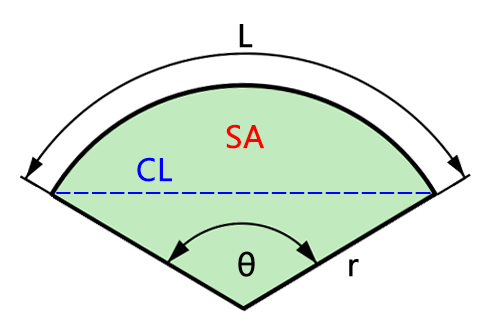
扇形是由圆心角分割出的圆的一部分，包含弧长和两条从圆心到圆弧的半径。根据扇形的半径 \( r \) 和圆心角 \( \theta \)（度数或弧度），可以计算出扇形的各种属性。

如何计算扇形的各个参数？

弧长计算

弧长表示扇形边界上弯曲部分的长度。

• 若角度 \( \theta \) 为度数，则弧长： \( L = 2 \pi r \times \frac{\theta}{360} \)
• 若角度 \( \theta \) 为弧度，则弧长： \( L = r \times \theta \)

弦长计算

弦长表示连接扇形两端的直线的长度。 \( c = 2r \times \sin\left(\frac{\theta}{2}\right) \) 若角度为度数，需将 \( \theta \) 转为弧度 \( \left(\theta \times \frac{\pi}{180}\right) \) 计算。

面积计算

面积 \( A \)：表示扇形的表面积。

• 若角度 \( \theta \) 为度数，面积： \( A = \pi r^2 \times \frac{\theta}{360} \)
• 若角度 \( \theta \) 为弧度，面积： \( A = \frac{1}{2} r^2 \theta \)

示例：已知半径 \( r = 10 \) 且圆心角 \( \theta = 60^\circ \)，计算弧长、弦长和面积。