中点计算器
输入两个坐标,快速计算这两个坐标的中点位置。
中点坐标计算
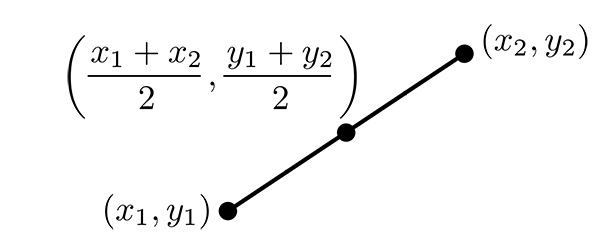
第一个点
第二个点
中点坐标
什么是中点?
在平面几何中,中点是连接两点的线段的中心位置。对于给定的两个坐标点 \( (x_1, y_1) \) 和 \( (x_2, y_2) \),可以计算出它们的中点 \( M \) 的坐标。
如何计算中点?
假设两点的坐标分别为 \( (x_1, y_1) \) 和 \( (x_2, y_2) \),则中点 \( M(x, y) \) 的坐标为: \( x = \frac{x_1 + x_2}{2} \) \( y = \frac{y_1 + y_2}{2} \)
示例
例子 1:已知点 \( A(2, 3) \) 和点 \( B(8, 7) \),求中点 \( M \)。
解答:
\( x = \frac{2 + 8}{2} = 5 \)
\( y = \frac{3 + 7}{2} = 5 \)
结果:中点 \( M(5, 5) \)
例子 2:已知点 \( C(-4, 6) \) 和点 \( D(10, -2) \),求中点 \( M \)。
解答:
\( x = \frac{-4 + 10}{2} = 3 \)
\( y = \frac{6 + (-2)}{2} = 2 \)
结果:中点 \( M(3, 2) \)