Welcome to the Heronian mean calculator which calculates the Heronian mean of two positive numbers.
What is Heronian mean?
The Heronian mean is an average of two non-negative real numbers, represented by H, and its formula is
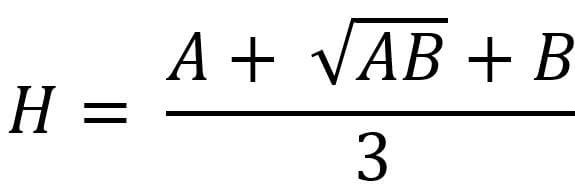 The Heronian mean can also be regarded as the weighted mean of the arithmetic mean and the geometric mean. The corresponding weights are 23 and 13. The formula is as follows
The Heronian mean can also be regarded as the weighted mean of the arithmetic mean and the geometric mean. The corresponding weights are 23 and 13. The formula is as follows

How to calculate the Heronian mean?
- Calculate the product of two non-negative numbers.
AB
- Find the square root of a product.
√AB
- Find the sum of two numbers.
A + B
- Calculate the Heronian mean
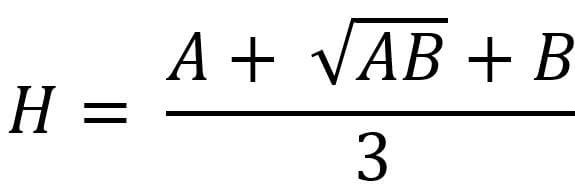
For example, what is the Heronian mean of 3 and 12?
H = 3 + √3*12 + 123 = 213 = 7
How to use the Heronian mean calculator
Using the calculator is simple, follow these 2 steps:
- Enter non-negative numbers in the first and second input boxes, respectively.
- Click Calculate button to calculate the Heronian mean of the two numbers, or click Reset button to start a new calculation.
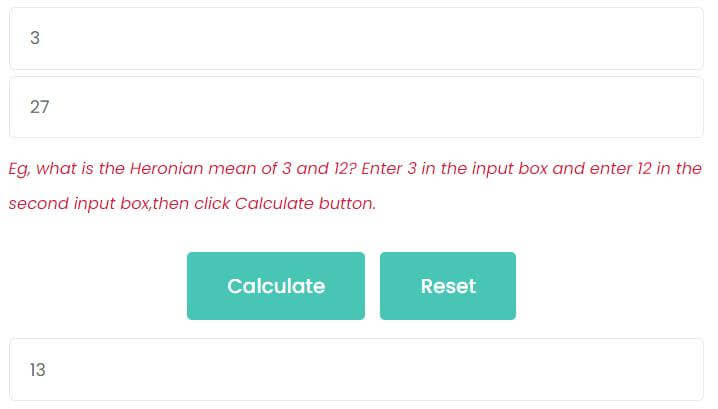
For example, find the Heronian mean of 3 and 27.
Enter 3 in the first input box.
Enter 27 in the second input box.
Then, click Calculate button. As the picture shows, the Heronian mean is 13.
Latest Calculators
Standard Form to Slope-Intercept Form Calculator
Slope Intercept Form Calculator
Slope Calculator: Calculate Slope, X-Intercept, Y-Intercept
Reciprocal of Complex Number Calculator
Conjugate Complex Number Calculator
Modulus of Complex Number Calculator
Profit Percentage Calculator: Calculate Your Profitability Easily
Attendance and Absence Percentage Calculator
Latest Checkers
Check if the given number is an almost perfect number.