Are you intrigued by the beauty and harmony found in nature, art, and architecture? One of the key principles behind this allure is the Golden Ratio. In this article, we will dive into the captivating realm of the Golden Ratio, its remarkable significance across different domains, and how our user-friendly online tool can effortlessly help you calculate it. Whether you’re a math enthusiast, an artist, or simply curious, this tool will help you unlock the secrets of harmonious proportions.
What is the Golden Ratio
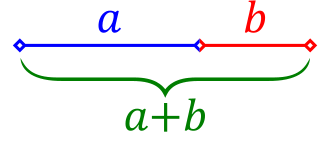
The Golden Ratio, denoted by the Greek letter phi (Φ), is an intriguing mathematical constant with an approximate value of 1.61803398875. It has fascinated mathematicians, artists, and scientists for centuries due to its unique properties. The Golden Ratio is found when the ratio of two quantities is equal to the ratio of their sum to the larger quantity. Its formula can be expressed as follows:
Φ = a + ba = ab
For example, cutting a line segment according to the golden ratio, the long part is 34, and what is the short part?
Step 1: According to the formula, we know that a=34, and b is the number to be calculated.
Step 2: Divide a by the golden ratio Φ (1.6180339887) to calculate b.
341.6180339887 = 21
So, the short part is 21, The total length of the line segment is 34 + 21 = 55.
What is the Golden Ratio Calculator
Our Golden Ratio Calculator is your ultimate tool to explore this mesmerizing ratio. Whether you’re delving into art, architecture, or nature’s wonders, our calculator will help you unveil the beauty of the Golden Ratio with ease. By entering a single number into the calculator, you can instantly discover the two other numbers that maintain the Golden Ratio with your input.
How to Use the Golden Ratio Calculator
Using our Golden Ratio Calculator is a breeze. Here’s a quick guide:
- Select the type you want to input. Long part (a), short part (b) or whole (a+b).
- Enter the a positive number.
- Click the Calculate button to obtain the other numbers.
- Click the Reset button to start a new calculation
FAQs
- Q: What is the significance of the Golden Ratio in nature?A: The Golden Ratio appears abundantly in nature, from the spiral arrangement of sunflower seeds to the shape of seashells and even the human body proportions. It is believed that nature adopts this ratio because of its inherent sense of balance and harmony, making it visually appealing.
- Q: How is the Golden Ratio connected to the Fibonacci sequence?A: The Golden Ratio is intricately related to the Fibonacci sequence, where each number is the sum of the two preceding ones (e.g., 0, 1, 1, 2, 3, 5, 8, 13, …). As the sequence progresses, the ratio between consecutive numbers approaches the Golden Ratio (approximately 1.618).
Conclusion
In conclusion, the Golden Ratio Calculator is an invaluable tool for anyone seeking to explore the magic of harmonious proportions. Its user-friendly interface and accurate calculations make it accessible to experts and enthusiasts alike. Whether you’re an artist seeking perfect balance in your creations or a mathematician studying the beauty of ratios, the Golden Ratio Calculator will undoubtedly enrich your creative journey. Embrace the allure of the Golden Ratio and let its elegance inspire your work!
Latest Calculators
Standard Form to Slope-Intercept Form Calculator
Slope Intercept Form Calculator
Slope Calculator: Calculate Slope, X-Intercept, Y-Intercept
Reciprocal of Complex Number Calculator
Conjugate Complex Number Calculator
Modulus of Complex Number Calculator
Profit Percentage Calculator: Calculate Your Profitability Easily
Attendance and Absence Percentage Calculator
Trigonometric Functions
Arccsc Calculator – Find the Exact Value of Inverse Cosecant
Arcsec Calculator – Find the Exact Value of Inverse Secant
Arccot Calculator – Find the Exact Value of Inverse Cotangent
Arctan Calculator – Find the Exact Value of Inverse Tangent
Inverse Cosine Calculator – Find The Exact Value of Arccos
Inverse Sine Calculator – Find The Exact Value of Arcsin
Inverse Trigonometric Functions Calculator
Trigonometric Functions Conversion Calculator
Trig Calculator – Find 6 Trigonometric Functions by Angles or Sides