The fraction exponent calculator is an online tool used to calculate the value of fraction exponent in a matter of milliseconds.
What is a fractional exponent
Before dwelling into fraction exponents, understanding whole number exponents is important. The exponent is also called as index or power. The exponent form of a number indicates the number of times the number must be used in a multiplication.
For example, 84, read as 8 to the power 4 should be calculated by multiplying the number 8 four times. So, 84= 8 * 8 * 8 * 8 = 4096. In case, the exponent is 2, it is read as 8 squared. Calculate the whole number exponents value by Free Exponents Calculator
Now, if the exponent part is a fraction, then it is called fraction exponent or more commonly, fractional exponent. Fraction exponent is the short form to represent power and root in a combined manner. The fractional exponent is expressed as xm/n. Here, x is the base and m/n is the exponent, which is a fraction.
How to calculate the fraction exponents
To solve a fraction exponent, you need to combine the techniques of calculating power and root together. Knowing the terms of fraction exponent will help you to solve the problem.
In xm/n, you have to take the nth root of xm.
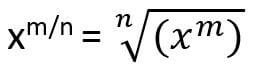
It is also the same as
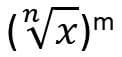
To solve this fraction exponent, you have to multiply x, m number of times and then take the nth root of the result.
In the expression xm/n , the radicand is the number specified under the radical sign. It is xm here. The index/order of the radical is the number representing the root that is taken. Here, index or order of radical is n. The base is the number for which root is taken. Here, the base is x. The power indicates the number of times the base must be multiplied in the fraction exponent expression before the root is taken. Here, the power is m.
To solve 642/3, you have to evaluate 3√642 which can be further simplified as (3√64)2.
642/3 = (3√64)2
= (3√43)2
= 42
= 16
Fractional exponents are much easier to solve if the value of m = 1. So, to solve x1/n, you simply have to take the nth root of x.
Below are some of the widely used fractional exponents:
- X1/2 = square root of x = √x
- X1/3 = cube root of x = 3√x
- X1/4 = fourth root of x = 4√x
Rules for fractional exponents
The laws of exponents can be extended and applied to fractional exponents. Instead of adding and subtracting whole numbers in the exponents part, you will be adding and subtracting fractions.
Same base and different exponents
- x1/m * x1/n = x(1/m + 1/n)
- x1/m ÷ x1/n = x(1/m – 1/n)
Different bases and same exponents
- x1/m * y1/m = (x * y)1/m
- x1/m ÷ y1/m = (x ÷ y)1/m
Negative fractional exponents
- x-m/n = (1/x)m/n
- (y/x)-m/n = (x/y)m/n
The fractional exponents can be simplified and evaluated if you understand the concepts of power and root. The fraction exponents can be solved following the above-mentioned rules even if the base is a fraction. This means that the same rules apply to solving (x/y)m/n.
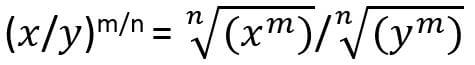
Negative fractional exponents
Evaluating negative fractional exponents is similar to evaluating rational exponents, but you need to take the reciprocal of the base to begin problem solving. Generally, when dealing with exponents, when the problem is x-m, you have to evaluate (1/x)m. In the same way, to evaluate x-m/n, you have to evaluate (1/x)m/n.
To solve 512-1/3, you have to evaluate (1/512)1/3.
512-1/3 = (1/512)1/3
= (1/83)1/3
= 1/8
Exponents with fractional bases
When the problem involves finding exponents of fractions, you have to evaluate the numerator and denominator separately. If the base is a fraction, you have to raise the numerator and denominator to the power separately and evaluate the answer.
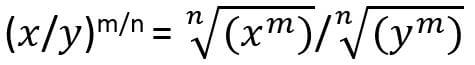
(121/144)1/2
= (2√121)/(2√144)
= (2√112)/(2√122)
= 11/12
Multiplication of fractional exponents
When the base is the same, you can multiply fraction exponents by adding the exponent fractions. When the bases are different, you have to evaluate each fraction exponent and then multiply the answers.
Base is the same
32/3 * 34/3 = 3(2/3+4/3) = 36/3
32/3 * 33/4 = 3(2/3+3/4) = 317/12
Bases are different
To evaluate 42/3 * 52/3, you have to evaluate 3√42 and 3√52 and then multiply both the answers.
Division of fractional exponents
To divide fraction exponent with the same base and different powers, you have to subtract the exponent fractions.
63/4 ÷ 62/3 = 63/4-2/3 = 61/12
To divide fraction exponent with different bases and the same powers, you have to divide the bases and then evaluate the power exponent.
83/4 ÷ 23/4 = (8 ÷ 2)3/4 = 43/4.
How to use the fraction exponent calculator
A fraction exponent calculator is an online tool that is designed to simplify evaluating fractional exponents. When the problem is too complex to solve on your own, you can seek the help of online tools to find answers quickly. The procedure to use the fraction exponent calculator is as follows:
- Enter the base into the first input box.
- Enter the numerator into the second input box.
- Enter the denominator into the third input box.
- Click the Calculate button to get the answer, click the Reset button to start a new calculation.
How to use the fraction exponent calculator
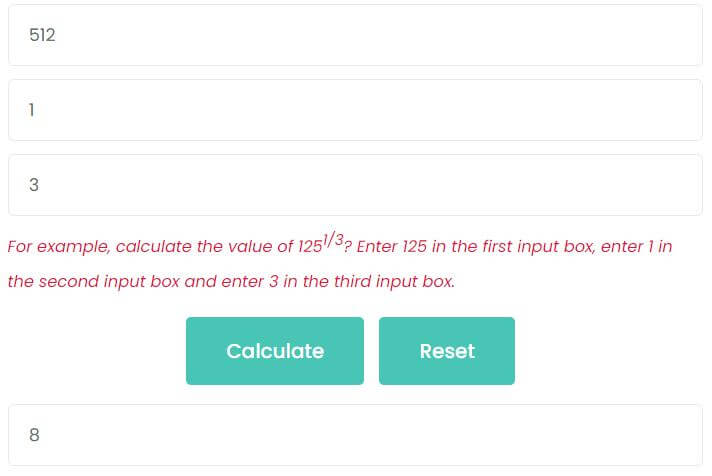
Example 1: calculate the value of 5121/3
- Enter 512 into the first and third input box.
- Enter 1 into the second input box.
- Enter 3 into the third input box.
- Finally, press Calculate button.
As the picture shows, the value of 5121/3 is 8.
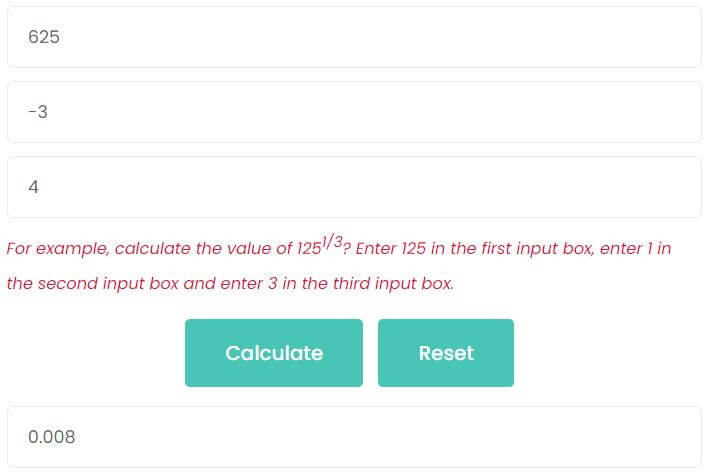
Example 1: calculate the value of 625-3/4
- Enter 625 into the first and third input box.
- Enter -3 into the second input box.
- Enter 4 into the third input box.
- Finally, press Calculate button.
As the picture shows, the value of 625-3/4 is 0.008.
Latest calculators
Standard Form to Slope-Intercept Form Calculator
Slope Intercept Form Calculator
Slope Calculator: Calculate Slope, X-Intercept, Y-Intercept
Reciprocal of Complex Number Calculator
Conjugate Complex Number Calculator
Modulus of Complex Number Calculator
Profit Percentage Calculator: Calculate Your Profitability Easily
Attendance and Absence Percentage Calculator
Circular Segment Radius Calculator
Regular Polygon Side Length Calculator
Annulus Calculator for Width, Perimeter, and Area
