The Euler’s Totient Function Calculator is a free online tool for calculating the value of Euler’s Totient function.
What is Euler's Totient function?
Euler’s totient function counts the positive integers up to a given integer n that are relatively prime to n. Indicated by φ(n). Relatively prime means the greatest common divisor of two integers is 1. The formula of Euler’s totient function is
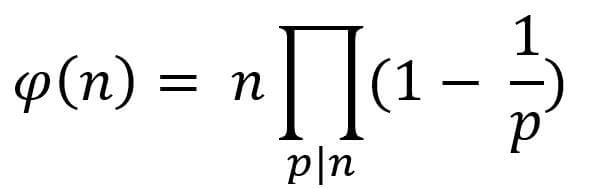 Where p represents all prime factors.
Where p represents all prime factors.
For example, What is the value of φ(12)?
Method 1: Calculate by normal
We know that the positive integers less than 12 are {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}. Among them, {1, 5, 7, 11} are relatively prime to 12. So, φ(12) = 4.
Method 2: Calculate by formula
With the prime factorization calculator, we can obtain the prime factorization of 12 is
12 = 22 * 3
So, the prime factors of 12 are 2 and 3. Put 2 and 3 into the formula
φ(12) = 12 * (1 – 12) * (1 – 13) = 12 * 12 * 23 = 6 * 23 = 4
Euler’s Totient function values corresponding to the first 100 positive integers
| φ(1) = 1 | φ(2) = 1 | φ(3) = 2 | φ(4) = 2 | φ(5) = 4 |
| φ(6) = 2 | φ(7) = 6 | φ(8) = 4 | φ(9) = 6 | φ(10) = 4 |
| φ(11) = 10 | φ(12) = 4 | φ(13) = 12 | φ(14) = 6 | φ(15) = 8 |
| φ(16) = 8 | φ(17) = 16 | φ(18) = 6 | φ(19) = 18 | φ(20) = 8 |
| φ(21) = 12 | φ(22) = 10 | φ(23) = 22 | φ(24) = 8 | φ(25) = 20 |
| φ(26) = 12 | φ(27) = 18 | φ(28) = 12 | φ(29) = 28 | φ(30) = 8 |
| φ(31) = 30 | φ(32) = 16 | φ(33) = 20 | φ(34) = 16 | φ(35) = 24 |
| φ(36) = 12 | φ(37) = 36 | φ(38) = 18 | φ(39) = 24 | φ(40) = 16 |
| φ(41) = 40 | φ(42) = 12 | φ(43) = 42 | φ(44) = 20 | φ(45) = 24 |
| φ(46) = 22 | φ(47) = 46 | φ(48) = 16 | φ(49) = 42 | φ(50) = 20 |
| φ(51) = 32 | φ(52) = 24 | φ(53) = 52 | φ(54) = 18 | φ(55) = 40 |
| φ(56) = 24 | φ(57) = 36 | φ(58) = 28 | φ(59) = 58 | φ(60) = 16 |
| φ(61) = 60 | φ(62) = 30 | φ(63) = 36 | φ(64) = 32 | φ(65) = 48 |
| φ(66) = 20 | φ(67) = 66 | φ(68) = 32 | φ(69) = 44 | φ(70) = 24 |
| φ(71) = 70 | φ(72) = 24 | φ(73) = 72 | φ(74) = 36 | φ(75) = 40 |
| φ(76) = 36 | φ(77) = 60 | φ(78) = 24 | φ(79) = 78 | φ(80) = 32 |
| φ(81) = 54 | φ(82) = 40 | φ(83) = 82 | φ(84) = 24 | φ(85) = 64 |
| φ(86) = 42 | φ(87) = 56 | φ(88) = 40 | φ(89) = 88 | φ(90) = 24 |
| φ(91) = 72 | φ(92) = 44 | φ(93) = 60 | φ(94) = 46 | φ(95) = 72 |
| φ(96) = 32 | φ(97) = 96 | φ(98) = 42 | φ(99) = 60 | φ(100) = 40 |
How to use the Euler's Totient function calculator
The procedure to use the Euler’s Totient function calculator is as follows:
- Enter the positive integer n.
- Click Calculate button to calculate the value of Euler's Totient function n.
- Click the Reset button to start a new calculation.
Solved examples using the Euler's Totient function calculator
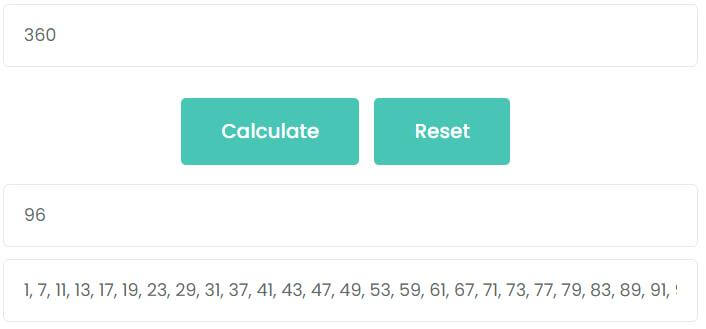
Example 1: Find φ(360) value.
Enter 360 into the input box and click Calculate button, as shown in the figure, the value of φ(360) is 96.
φ(360) = 96
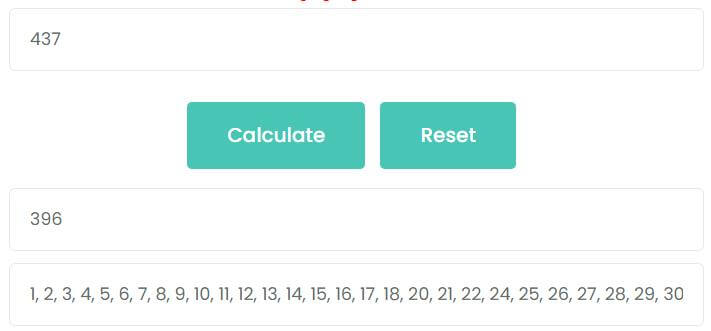
Example 2: What is the value of φ(437)?
Enter 437 into the input box and click Calculate button, as shown in the figure, the value of φ(437) is 396.
φ(437) = 396
Latest calculators
Standard Form to Slope-Intercept Form Calculator
Slope Intercept Form Calculator
Slope Calculator: Calculate Slope, X-Intercept, Y-Intercept
Reciprocal of Complex Number Calculator
Conjugate Complex Number Calculator
Modulus of Complex Number Calculator
Profit Percentage Calculator: Calculate Your Profitability Easily
Attendance and Absence Percentage Calculator
Circular Segment Radius Calculator
Regular Polygon Side Length Calculator
Annulus Calculator for Width, Perimeter, and Area