Welcome to the decimal to fraction calculator, where you can easily convert decimals into fractions, including improper fractions and mixed fractions.
What are decimals and fractions?
Before conversion, we should understand what is a decimal and what is a fraction?
Decimal is a special form of real number, usually composed of 3 parts: integer part, decimal point and decimal part. The decimal point is in the middle of integer and decimal.
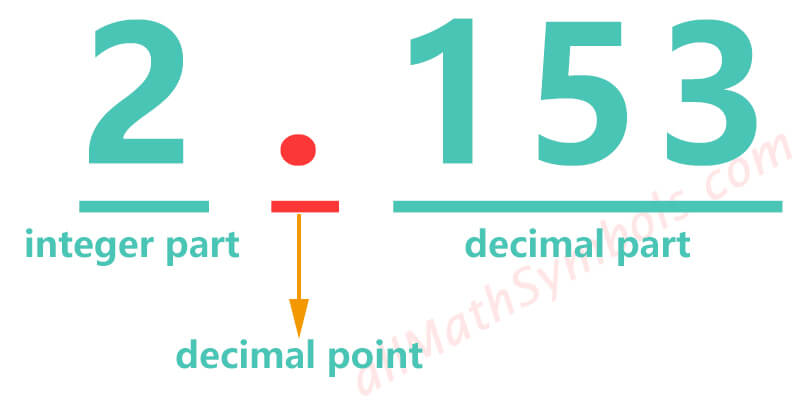 Among them, the number whose integer part is zero is called pure decimal. Numbers whose integer part is not zero are called mixed decimals. For example, 0.25 is a pure decimal, 1.53 is a mixed decimal.
Among them, the number whose integer part is zero is called pure decimal. Numbers whose integer part is not zero are called mixed decimals. For example, 0.25 is a pure decimal, 1.53 is a mixed decimal.
According to the length of the decimal part, it can be divided into finite decimals and infinite decimals. Infinite decimals include: infinite recurring decimals and infinite non-recurring decimals. Such as, 0.25 is a finite decimal, 0.3 is an infinite recurring decimal. The mathematical symbols π and e are infinite non-recurring decimals. Here, we mainly discuss two kinds of more commonly used decimals, finite decimals and infinite recurring decimals.
Fraction refers to the fraction of a number to another number, or the ratio of an event to all events. The numerator at the top and the denominator at the bottom. For example, 25 means that a whole number is divided into five equal parts, and 2 of them are taken. Usually, decimals and fractions can be converted to each other, let’s see how they are converted.
How to convert decimals into fractions?
The following 4 steps are required to convert decimals to fractions:
- Convert the decimal to an integer equation.
- Convert integer equations into a fraction.
- Find the greatest common divisor of the numerator and denominator in the fraction.
- Simplify the fraction and complete the conversion.
Let’s explain in detail how each step is operated.
Step 1. Convert the decimal to an integer equation
What does that mean? How to convert the decimal to an integer? It’s very simple, just multiply it by the Nth power of 10, where N represents the length of decimal part. For example, 0.25, the length of fractional part is 2, so 0.25 multiplied by the square of 10 can be converted into an integer.
0.25 * 102 = 25.
For another example, 1.3452 has 4 decimal places, so multiply by 10 to the 4th power.
1.3452 * 104 = 13452.
At this point, some people may have questions: What if it is an infinite recurring decimal? The length of the decimal is infinite. How to express the Nth power of 10? Don’t worry, there is a separate chapter below to explain in detail, you just need to remember this step: convert the decimal to an integer equation.
Step 2: Convert the integer equation to the fraction
We have already converted the decimal into an integer equation in step 1. At this time, both sides are divided by the Nth power of 10 to get the initial form of decimal to fraction.
0.25 * 102 = 25
0.25 = 25102
0.25 = 25100
25100 is the initial fraction form of decimal 0.25.
Step 3: Find the greatest common divisor
In step 2 we have obtained the initial form of the score. Now, we need to simplify the fraction. Therefore, we must find the greatest common divisor of the numerator and denominator first. The greatest common divisor of 25 and 100 is 25.
Step 4: Simplify the fraction
With the greatest common divisor, we can simplify the fraction
0.25 = 25100 = 14
Therefore, the fraction form of 0.25 is 14.
This is the complete conversion steps from decimal to fraction. According to these 4 steps, the conversion from decimal to fraction can be realized.
Convert decimals to fractions examples
What is 0.06 as a fraction?
According to the 4 steps provided above
0.06 * 102 = 6
0.06 * 100 = 6
0.06 = 6100
6100 is the initial fraction form of decimal 0.06. Next, find the greatest common divisor of 6 and 100. Their greatest common divisor is 2.
0.06 = 6100
0.06 = 350
So, the fraction form of 0.06 is 350.
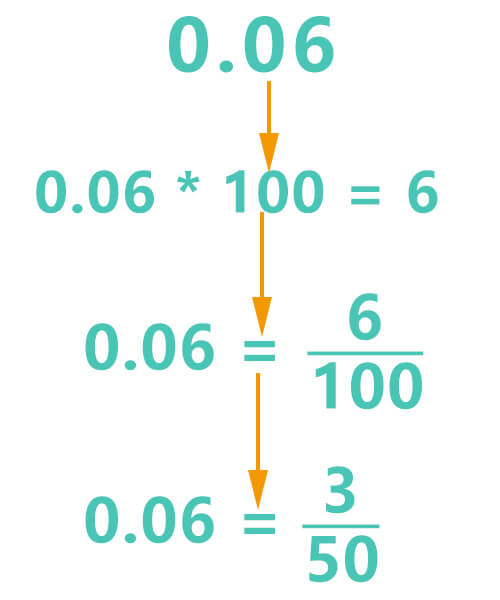
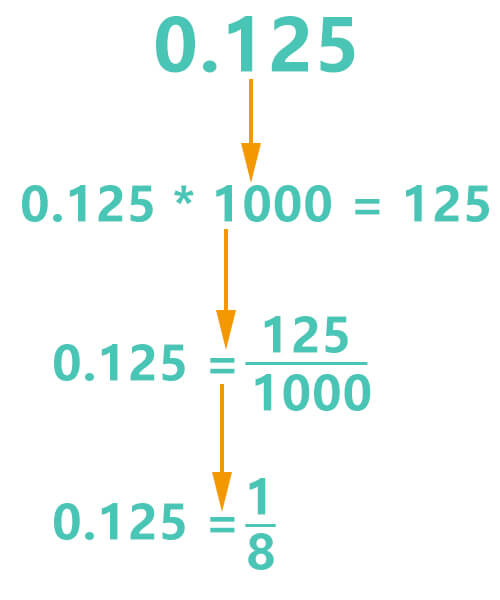
What is 0.125 as a fraction?
According to the 4 steps provided above
0.125 * 103 = 125
0.125 * 1000 = 125
0.125 = 1251000
1251000 is the initial fraction form of decimal 0.125. Next, find the greatest common divisor of 125 and 1000. Their greatest common divisor is 126.
0.125 = 1251000
0.125 = 18
So, the fraction form of 0.125 is 18.
What is 3.1465 percent as a fraction?
According to the 4 steps provided above
3.1465 * 104 = 31465
3.1465 * 10000 = 31465
3.1465 = 3146510000
3146510000 is the initial fraction form of decimal 3.1465. Next, find the greatest common divisor of 31465 and 10000. Their greatest common divisor is 5.
3.1465 = 3146510000
3.1465 = 62932000
3.1465 = 32932000
So, the fraction form of 3.1465 is 32932000.

It can be seen that these conversion steps are also applicable to decimals greater than 1. When it is a decimal greater than 1, the converted fraction is an improper fraction, and after simplification, it is a mixed fraction.
Wait, did you forget another question? How to convert an infinite recurring decimal to a fraction? The next content is the key part.
How to convert an infinite recurring decimal into a fraction?
Follow the first step above to convert fractions to integers. So, how to convert an infinite recurring decimal into an integer? Let’s start with a few examples.
Example 1:
0.6, there is 1 trailing decimal place is repeated. Let x is equal to 0.6, then 10 * x = 6.6.
10x – x = 6.6 – 0.6
9x = 6
x = 69
69 is the initial fraction form of decimal 0.6. Next, find the greatest common divisor and simplify it to complete the conversion.
Example 2:
1.23, repeat with 2 trailing decimal places. Suppose x is equal to 1.23, then 100x = 123.23, so
100x – x = 123.23 – 1.23
99x = 122
x = 12299
12299 is the initial fraction form of decimal 1.23. Now, find the greatest common divisor and simplify it to complete the conversion.
Example 3:
3.102, repeat with 3 trailing decimal places. Suppose x is equal to 3.102, then 1000x = 3102.102, so
1000x – x = 3102.102 – 3.102
999x = 3102 – 3
x = 3099999
3099999 is the initial fraction form of decimal 3.102, and the next step is to simplify the fraction.
Did you find any rules through observation?
Yes, the number of digits in the denominator is related to the number of trailing decimal places to repeat. Repeat with 1 trailing decimal place, the denominator is a 9. Repeat with 2 trailing decimal places, the denominator is 99. Repeat with 3 trailing decimal places, the denominator is 999. By analogy, repeat with N trailing decimal places, the denominator is contained N 9s.
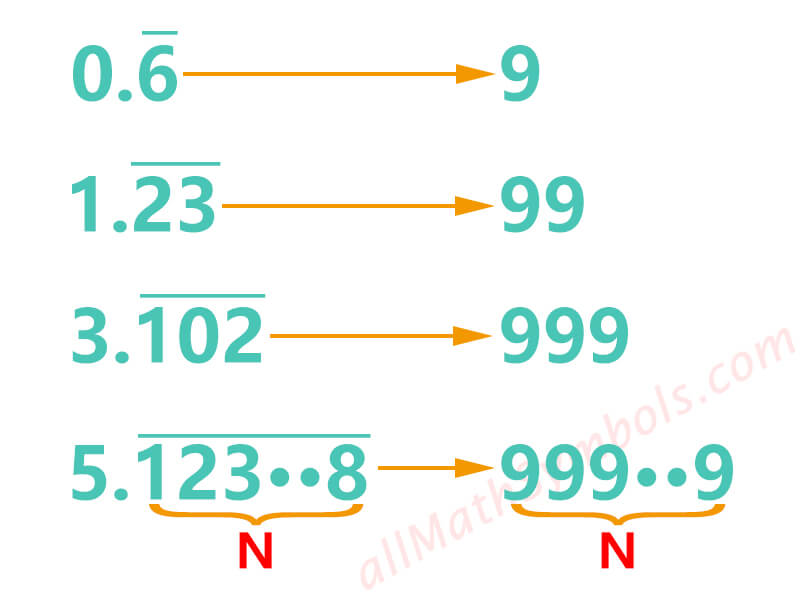 So, what about the numerator? The numerator is equal to the number consisting of the whole number part and the trailing decimal places to be repeated minus the whole number part.
So, what about the numerator? The numerator is equal to the number consisting of the whole number part and the trailing decimal places to be repeated minus the whole number part.
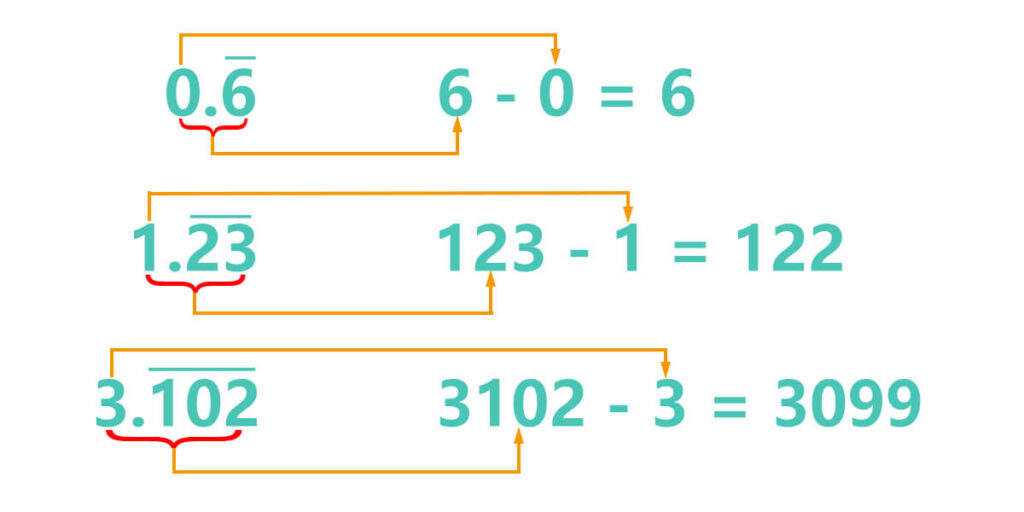
- 0.6, the whole number part is 0, the trailing decimal place to be repeated is 6. So the numerator is 6 – 0 = 6.
- 1.23, the whole number part is 1, the trailing decimal place to be repeated is 23. so the numerator is 123 – 1 = 122.
- 3.102, the whole number part is 3, the trailing decimal place to be repeated is 102. So the numerator is 3102 – 3 = 3099.
Therefore, when the decimal point is immediately followed by the trailing decimal places to be repeated, the general formula for converting infinite loop decimals to fractions can be described as:
Numerator: Number composed of the integer part and the trailing decimal places to be repeated minus the integer partDenominator: N 9s
N represents the number of trailing decimal places to be repeated.
Another infinite repeating decimal to fraction
Wait a moment, the above three examples are all trailing decimal places to be repeated immediately after the decimal point. If there are other non-recurring decimal places after the decimal point, can the above general formula be used? Similarly, let’s analyze through several examples.
Example 1:
0.13, the decimal point is followed by an non-recurring decimal place of 1, and then followed by a repeating trailing decimal place of 3. Let x = 0.13, then 10x = 1.3, 100x = 13.3
100x – 10x = 13.3 – 1.3
90x = 12
x = 1290
1290 is the initial fraction form of decimal 0.13.
Example 2
0.213, the decimal point is followed by two non-recurring decimal places of 21, and then followed by a repeating trailing decimal place of 3. Let x = 0.213, then 100x = 21.3,1000x = 213.3
1000x – 100x = 213.3 – 21.3
900x = 192
x = 192900
192900 is the initial fraction form of decimal 0.213.
Example 3
2.3513, the decimal point is followed by two non-recurring decimal places of 35, and then followed by two repeating trailing decimal places of 13. Let x = 2.3513, then 100x = 235.13,10000x = 23513.13
10000x – 100x = 23513.13 – 235.13
9900x = 23513 – 235
x = 232789900
232789900 is the initial fraction form of decimal 2.3513.
Example 4
8.1233153, the decimal point is followed by four non-recurring decimal places of 1233, and then followed by three repeating trailing decimal places of 153. Let x = 8.1233153, then 10000x = 81233.153,10000000x = 81233153.153
10000000x-10000x = 81233153.153 – 81233.153
9990000x = 81233153 – 81233
x = 811519209990000
811519209990000 is the initial fraction form of decimal 8.1233153.
Through the above 4 examples, we can see that the denominator is composed of 9 and 0. The number of 9 is consistent with the number of trailing decimal places to be repeated, and the number of 0 is consistent with the number of non-recurring decimal places.
 The numerator is a number composed of the integer part, non-recurring decimal places and the trailing decimal places to be repeated minus the number composed of the integer part and non-recurring decimal places.
The numerator is a number composed of the integer part, non-recurring decimal places and the trailing decimal places to be repeated minus the number composed of the integer part and non-recurring decimal places.

Conclusion
In summary, the conversion of decimals into fractions can be divided into 3 cases. The general formulas are as follows:
1. Finite decimals to fractions formula
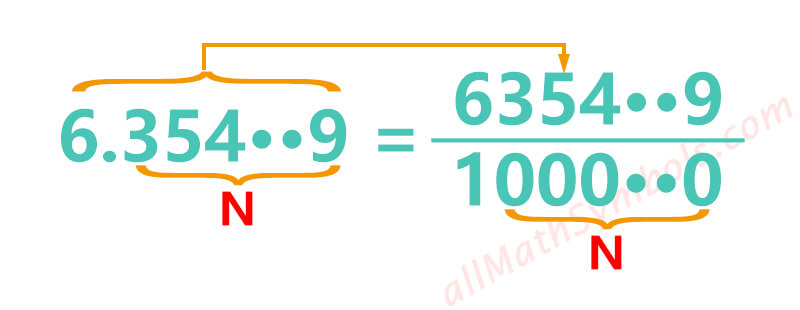
The initial fraction is:
The numerator is the number that removes the decimal point from decimals.The denominator is equal to the Nth power of 10, where N represents the length of decimal part.
2. Infinite recurring decimals to fractions formula one
The decimal point is immediately followed by the trailing decimal places to be repeated.
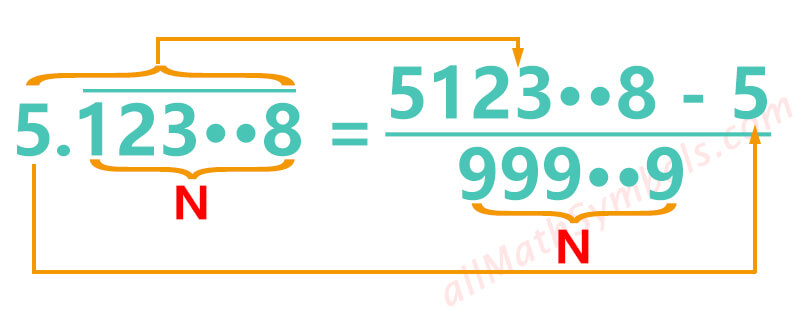
The initial fraction is:
The numerator is composed of the integer part and the trailing decimal places to be repeated minus the integer part.The denominator is N 9s, where N represents the number of trailing decimal places to be repeated.
3. Infinite recurring decimals to fractions formula two
The decimal point is followed by the non-recurring decimal places and then the trailing decimal places to be repeated.
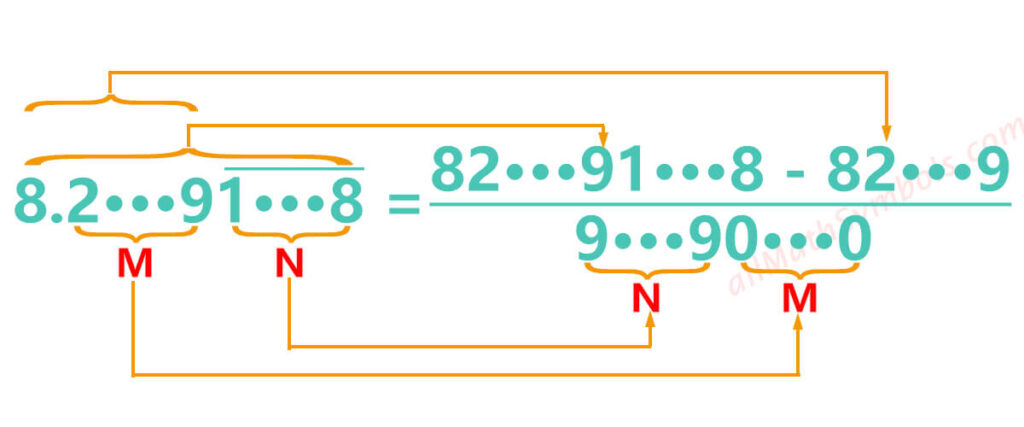
The initial fraction is:
The numerator is a number composed of the integer part, non-recurring decimal places and the trailing decimal places to be repeated minus the number composed of the integer part and non-recurring decimal places.The denominator is composed of 9 and 0. The number of 9 is consistent with the number of trailing decimal places to be repeated, and the number of 0 is consistent with the number of non-recurring decimal places.
This is the complete content of converting decimals to fractions. The content is complex and recommended to read it several times. If you don’t understand, leave a message for discussion. Of course, if possible, you can use the decimal to fraction calculator provided above directly, which can help you save these tedious steps.
How to use the decimal to fraction calculator?
The calculator is very simple to use, enter decimals. If it is an infinite recurring decimal, enter the number of trailing decimal places to be repeated, and then click calculate button. The answer will be presented within milliseconds.
Solved examples using decimal to fraction calculator
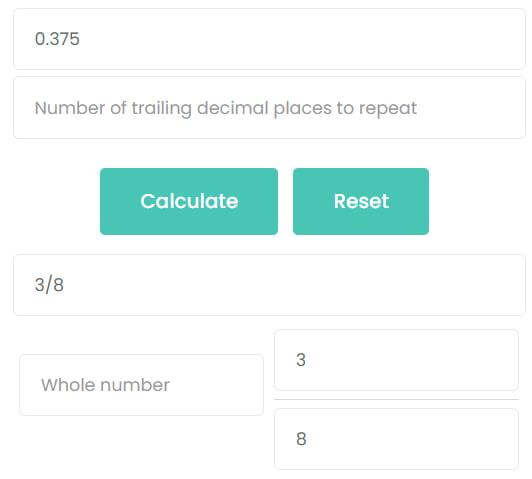
What is 0.375 as a fraction?
0.375 is a finite decimal, which can be converted by the first formula summarized above
0.375 = 3751000 = 38
The second method: calculate by calculator. Enter 0.375 into the first input box and click calculate. You can see that the answer is also 38.
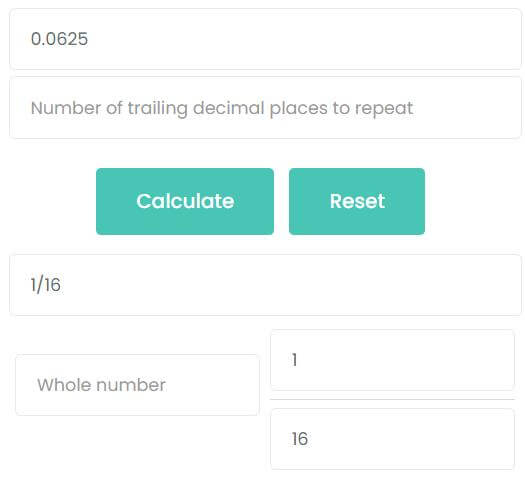
What is 0.0625 as a fraction?
0.0625 is a finite decimal, which can be converted by the first formula summarized above
0.0625 = 62510000 = 116
The second method: calculate by calculator. Enter 0.0625 into the first input box and click calculate. You can see that the answer is also 116.
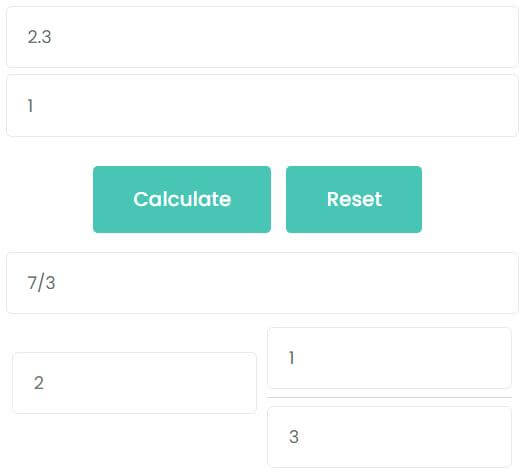
How to convert 2.3 to a fraction?
2.3 is an infinite recurring decimal, the decimal point is immediately followed by the trailing decimal places to be repeated. Therefore, use the second formula summarized above to convert to the fraction
2.3 = 23 – 29 = 219 = 73
The second method: calculate by calculator. There is 1 repeated trailing decimal place. So, enter 2.3 into the first input box and enter 1 into the second input box, then click calculate. You can see that the answer is also 73.
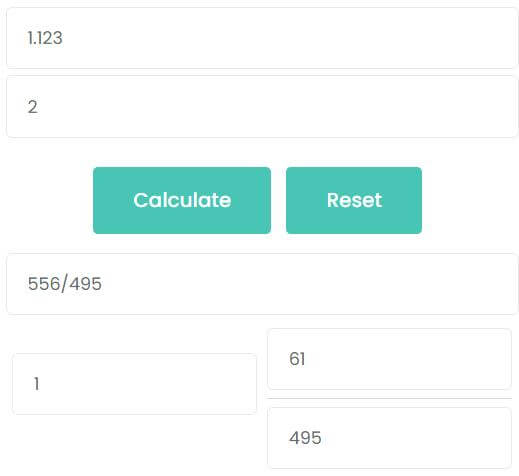
How to convert 1.123 to a fraction?
1.123 is an infinite recurring decimal, the decimal point is followed by the non-recurring decimal places. Therefore, use the third formula summarized above to convert to the fraction
1.123 = 1123 – 11990 = 1112990 = 556495
The second method: calculate by calculator. There is 1 non-recurring decimal place and 2 repeated trailing decimal places. So, enter 1.123 into the first input box and enter 2 into the second input box, then click calculate. You can see that the answer is also 556495.
Latest calculators
Standard Form to Slope-Intercept Form Calculator
Slope Intercept Form Calculator
Slope Calculator: Calculate Slope, X-Intercept, Y-Intercept
Reciprocal of Complex Number Calculator
Conjugate Complex Number Calculator
Modulus of Complex Number Calculator
Profit Percentage Calculator: Calculate Your Profitability Easily
Attendance and Absence Percentage Calculator
Circular Segment Radius Calculator
Regular Polygon Side Length Calculator
Annulus Calculator for Width, Perimeter, and Area