The Cubic Mean Square Calculator is a free online tool to calculate the cubic mean of a data set. The number in the data set is not limited, it can be one number or multiple numbers. It can be an integer, a decimal, or even a fraction.
What is the cubic mean?
There are many kinds of average values, such as arithmetic mean, geometric mean, root mean square, etc. The cubic mean is also a kind of average value, which is to take the average of the sum of the cubes of a set of data, and then find the cube root. The cubic mean is especially useful when the relationship between the function and the independent variable is cubic, such as wind energy and wind speed.
The formula for the cubic mean is as follows
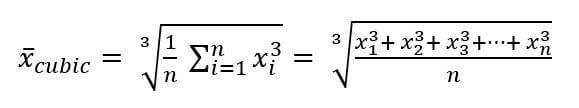 Among them, n represents the length of the dataset, xi is each number in the dataset.
Among them, n represents the length of the dataset, xi is each number in the dataset.
How to calculate the cubic mean?
As can be seen from the above formula, at least 4 steps are required to obtain the cubic mean.
- Calculate the cubic value.
- Sum of cubes.
- Calculate the average.
- Find the cube root.
For example, what is the cubic mean for dataset {1, 5, 8, 10}?
First, cube of each number.
13 = 1
53 = 125
83 = 512
103 = 1000
Second, sum of cubes.
1 + 125 + 512 + 1000 = 1638
Third, calculate the average
16384 = 409.5
Finally, calculate the cube root.
3√409.5 = 7.43
So, the cubic mean for dataset {1, 5, 8, 10} is 7.43.
How to use the cubic mean calculator
To use the Cubic Mean Calculator, you have to prepare your data first, and then enter them into the calculator’s input box. One number per line or separate each number with a comma. After all the data input is complete, click the Calculate button, and the cubic mean will appear in a blink of an eye.
FAQS
- Q: Can cubic mean be zero or negative?A: Yes, it is possible, it depends on your data.
- Q: What is the cubic mean calculator?A: As the name suggests, it is a calculator used to calculate the cubic mean.
- Q: Why would I need to use the cubic mean calculator?A: You need it, no doubt. Because the calculation of the cubic mean is relatively large, such as the cube or cube root of a number is difficult to calculate manually. It’s even more troublesome if there are decimals or fractions. So, you should urgently need a cubic mean calculator.
- Q: Can I enter decimals or fractions?A: Yes, sure. Remember to separate data by our convention (comma or new line).
- Q: How many numbers can be entered at one time?A: There is no limit, according to your actual situation, it can be 100, 1000, or even more.
Conclusion
In short, the cubic mean is a complicated calculation. You can easily find the sum of cubes of numbers, but it is not so easy to calculate the cube root of a number. So, we developed this cubic mean calculator to help you find the cubic mean easily and quickly. Hurry to try it.
Latest Calculators
Standard Form to Slope-Intercept Form Calculator
Slope Intercept Form Calculator
Slope Calculator: Calculate Slope, X-Intercept, Y-Intercept
Reciprocal of Complex Number Calculator
Conjugate Complex Number Calculator
Modulus of Complex Number Calculator
Profit Percentage Calculator: Calculate Your Profitability Easily
Attendance and Absence Percentage Calculator
Latest Checkers
Check if the given number is an almost perfect number.