Welcome to the Arc Radius Calculator, a handy tool designed to help you easily calculate the arc radius of a circular object. In this article, we will delve into the concept of arc radius, explain the formula, and provide step-by-step instructions along with real-life examples to ensure you have a clear understanding of how to use this powerful tool.
What is Arc Radius
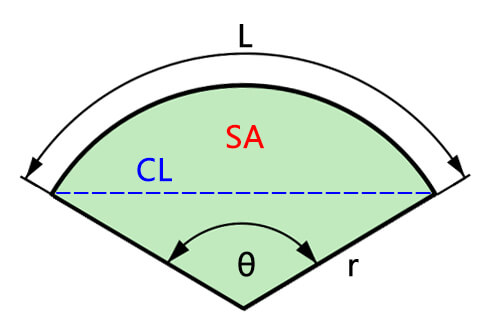
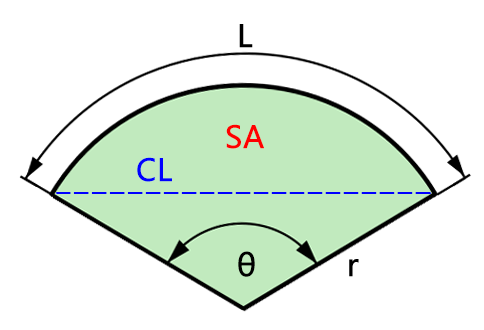
In geometry, an arc is a curved segment of a circle. The arc radius refers to the distance from the center of the circle to the arc. The formula for calculating the arc radius is derived from the arc length and the central angle. To calculate the arc radius, you need the arc length (L) and the central angle (θ) of the arc. The formula to find the arc radius (r) is straightforward and elegant:
r = Lθ
where:
- L = Arc length
- θ = Central angle in radians
How to Calculate Arc Radius
Let’s walk through a step-by-step example to calculate the arc radius. Suppose we have an arc with an arc length of 8 units and a central angle of 45 degrees.
Step 1: Convert the angle to radians.
θ = 45° = 45 * π180 = π4
Step 2: Plug the given values into the formula and simplify the equation.
r = 8π / 4 ≈ 10.186 units
What is the Arc Radius Calculator
The Arc Radius Calculator is a valuable tool for anyone dealing with circles and arcs. It streamlines the process of finding the radius of an arc, eliminating the need for manual calculations. Whether you’re a student, a professional, or just curious about arcs, this calculator simplifies your work and ensures precise results.
How to Use the Calculator
Using the Arc Radius Calculator is a breeze. Follow these simple steps to find the arc radius:
- Enter the arc length (L) in the designated input box.
- Input the central angle (θ) in the provided field.
- Select angle type, degrees or radians.
- Click on the Calculate button to obtain the arc radius.
Solved Examples
Example 1: Find the arc radius when the arc length is 12 units and the central angle is 60 degrees.
Solution:
θ = 60° = π3
r = 12π/3 = 11.459 units
Example 2: Determine the arc radius with an arc length of 10 units and a central angle of 30 degrees.
Solution:
θ = 30° = π6
r = 10π/6 = 19.1 units
FAQs
- Q: Can the arc radius ever be negative?A: No, the arc radius is always a positive value, representing the distance from the center of the circle to the arc.
- Q: Is it possible to have an arc with a zero radius?A: No, a zero radius would indicate a point rather than an arc.
- Q: How does the arc radius affect the size of the arc?A: The arc radius determines the curvature of the arc; a larger radius results in a more gentle curve, while a smaller radius creates a sharper arc.
- Q: Can I use the Arc Radius Calculator for finding the radius of any arc?A: Yes, this calculator is applicable to all circular arcs regardless of their size.
- Q: What happens if the central angle is 180 degrees?A: If the central angle is 180 degrees, the arc forms a semicircle, and the radius is equal to half the diameter of the circle.
- Q: Can I use the calculator for non-circular arcs?A: No, the calculator is specifically designed for circular arcs only.
- Q: How precise are the results obtained from the Arc Radius Calculator?A: The calculator provides highly accurate results, ensuring that you get reliable measurements for your arcs.
- Q: What are the applications of the arc radius calculator?A: The arc radius calculator has a wide range of applications in various fields, including geometry, engineering, architecture, and graphic design. It is commonly used to calculate the dimensions of circular objects, such as arcs, circles, and curves, which are prevalent in architectural designs, automotive engineering, and computer graphics.
- Q: Can I use degrees instead of radians for the central angle?A: Yes. Select the corresponding type in the calculator!
Latest Calculators
Standard Form to Slope-Intercept Form Calculator
Slope Intercept Form Calculator
Slope Calculator: Calculate Slope, X-Intercept, Y-Intercept
Reciprocal of Complex Number Calculator
Conjugate Complex Number Calculator
Modulus of Complex Number Calculator
Profit Percentage Calculator: Calculate Your Profitability Easily
Attendance and Absence Percentage Calculator
Trigonometric Functions
Arccsc Calculator – Find the Exact Value of Inverse Cosecant
Arcsec Calculator – Find the Exact Value of Inverse Secant
Arccot Calculator – Find the Exact Value of Inverse Cotangent
Arctan Calculator – Find the Exact Value of Inverse Tangent
Inverse Cosine Calculator – Find The Exact Value of Arccos
Inverse Sine Calculator – Find The Exact Value of Arcsin
Inverse Trigonometric Functions Calculator
Trigonometric Functions Conversion Calculator
Trig Calculator – Find 6 Trigonometric Functions by Angles or Sides