Versine Calculator

Calculate the versine of any degrees or radians.

Welcome to the Versine Calculator! In this article, we will delve into the concept of the versine and its calculator. Whether you’re a math enthusiast, a student, or simply curious about trigonometric functions, this article will guide you through the fundamentals of the versine and how to calculate it using the Versine Calculator. Let’s dive in!

Versine Calculator

Calculate Reset

What is Versine

The versine function is related to the cosine function. It is sometimes denoted as versin or ver. It is defined as the complement of the cosine function. In other words, the versine of an angle is equal to 1 minus the cosine of that angle. Mathematically, it can be represented as:

Versine(x) = 1 – cos(x)

So, the versine function is derived from the cosine function and provides a different perspective on the relationship between angles and their corresponding trigonometric values. The range of the versine function is [0, 2], meaning it can take on any value within this interval, depending on the input angle.

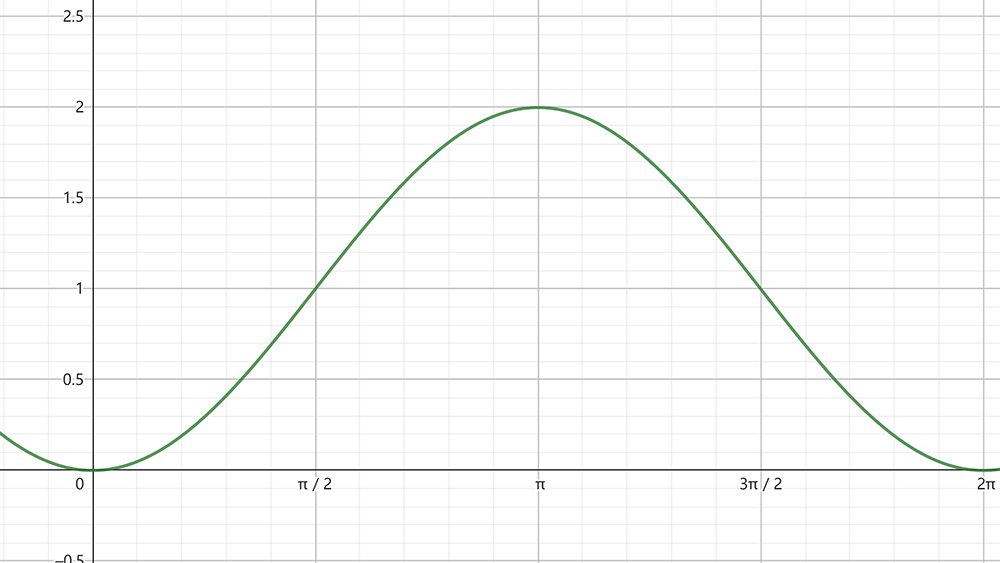
versine graph

For example, consider an angle of 45 degrees (π4 radians).

To find the versine, we substitute this value into the formula:

Versine(45°) = 1 – cos(45°)

Next, use the cosine calculator to calculate the value of cos(45°)

cos(45°) = 0.7071

Substitute values into the formula

Versine(45°) = 1 – cos(45°) = 1- 0.7071 = 0.2929

Therefore, the versine of the angle 45 degrees (π4 radians) is approximately 0.2929.

Versine Table

Degrees	Radians	Versine
0°	0	0
5°	π36	0.0038053
10°	π18	0.01519225
15°	π12	0.03407417
20°	π9	0.06030738
25°	5π36	0.09369221
30°	π6	0.1339746
35°	7π36	0.18084796
40°	2π9	0.23395556
45°	π4	0.29289322
50°	5π18	0.35721239
55°	11π36	0.42642356
60°	π3	0.5
65°	13π36	0.57738174
70°	7π18	0.65797986
75°	5π12	0.74118095
80°	4π9	0.82635182
85°	17π36	0.91284426
90°	π2	1
95°	19π36	1.08715574
100°	5π9	1.17364818
105°	7π12	1.25881905
110°	11π18	1.34202014
115°	23π36	1.42261826
120°	2π3	1.5
125°	25π36	1.57357644
130°	13π18	1.64278761
135°	3π4	1.70710678
140°	7π9	1.76604444
145°	29π36	1.81915204
150°	5π6	1.8660254
155°	31π36	1.90630779
160°	8π9	1.93969262
165°	11π12	1.96592583
170°	17π18	1.98480775
175°	35π36	1.9961947
180°	π	2
185°	37π36	1.9961947
190°	19π18	1.98480775
195°	13π12	1.96592583
200°	10π9	1.93969262
205°	41π36	1.90630779
210°	7π6	1.8660254
215°	43π36	1.81915204
220°	11π9	1.76604444
225°	5π4	1.70710678
230°	23π18	1.64278761
235°	47π36	1.57357644
240°	4π3	1.5
245°	49π36	1.42261826
250°	25π18	1.34202014
255°	17π12	1.25881905
260°	13π9	1.17364818
265°	53π36	1.08715574
270°	3π2	1
275°	55π36	0.91284426
280°	14π9	0.82635182
285°	19π12	0.74118095
290°	29π18	0.65797986
295°	59π36	0.57738174
300°	5π3	0.5
305°	61π36	0.42642356
310°	31π18	0.35721239
315°	7π4	0.29289322
320°	16π9	0.23395556
325°	65π36	0.18084796
330°	11π6	0.1339746
335°	67π36	0.09369221
340°	17π9	0.06030738
345°	23π12	0.03407417
350°	35π18	0.01519225
355°	71π36	0.0038053
360°	2π	0

What is Versine Calculator

The Versine Calculator is a handy tool designed to simplify the process of calculating the versine of any given angle. It eliminates the need for manual calculations, making it a time-saving and accurate solution for trigonometric computations.

How to Use the Versine Calculator

Using the Versine Calculator is straightforward. Follow these simple steps:

1Enter the desired angle value in the input box.
2Select the angle type, degrees or radians, the default is degrees.
3Click the Calculate button to obtain the result.
4Click the Reset button to start a new calculation

FAQs

Q: What is the range of the versine function?
A: The versine function has a range of [0, 2]. It can take on any value within this interval, depending on the input angle.

Q: How does the versine differ from the sine function?
A: While the sine function measures the vertical displacement of a point on the unit circle, the versine specifically calculates the vertical distance between a point on the circumference of a circle and the corresponding arc segment.

Q: What is the range of values for the input angle?
A: The input angle can be any real number, as the versine function is defined for all angles.

Q: Can the Versine Calculator handle both degrees and radians?
A: Yes, the Versine Calculator can handle input angles in both degrees and radians.

Q: Is the versine function commonly used in any specific field?
A: The versine function is primarily used in trigonometry and geometry. It finds applications in fields such as navigation, astronomy, and engineering where angles and their related calculations are involved.

Q: Can the Versine Calculator handle negative angle values?
A: Yes, the Versine Calculator can handle negative angle values. The versine function considers both positive and negative angles, and the output result will be based on the input angle provided.

Conclusion

Now, you’ve gained a solid understanding of the versine and its calculator. You now know how to calculate the versine of an angle using the formula and the convenient Versine Calculator. Whether you’re exploring trigonometry, working on mathematical problems, or pursuing academic studies, the versine is a valuable tool in your mathematical arsenal. Embrace the power of the versine and unlock new possibilities in your trigonometric adventures!