The Variance and Standard Deviation Calculator is a free online tool used to calculate the variance and standard deviation of a set of numbers.
What is variance?
In statistics, variance is the average of the sum of squares of the differences between the actual value and the expected value (the mean). Usually denoted by σ2. It is used to describe the degree of dispersion of a random variable. It occupies a very important position in statistics.
The expected value has a population mean or a sample mean, and different expected values have different calculation formulas.
The formula for population variance is
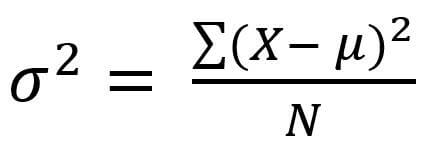 Among them, σ2 is the population variance, μ is the population mean, N is the total number of data.
Among them, σ2 is the population variance, μ is the population mean, N is the total number of data.
The formula for sample variance is
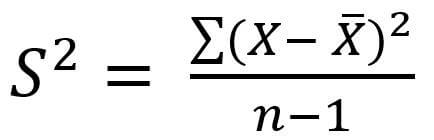 Where S2 is the sample variance, x is the sample mean, n is the total number of data.
Where S2 is the sample variance, x is the sample mean, n is the total number of data.
How to calculate variance?
There are several steps to calculating the variance:
First, find the sum of a set of numbers.
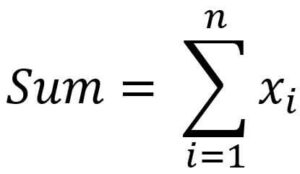 Second, calculate the arithmetic mean of the data set.
Second, calculate the arithmetic mean of the data set.
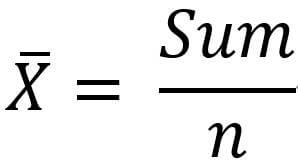 Third, calculate the squared difference of each data value from the mean.
Third, calculate the squared difference of each data value from the mean.
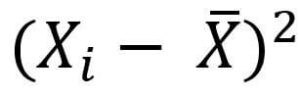 Fourth, add all the squared differences together.
Fourth, add all the squared differences together.
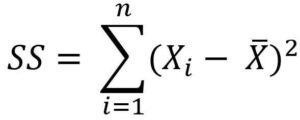 Fifth, calculate the population variance or sample variance, divide by N or n – 1.
Fifth, calculate the population variance or sample variance, divide by N or n – 1.
For example, a sample data [3, 5, 6, 8, 9, 5], find the variance.
Calculate the sum of the data
3 + 5 + 6 + 8 + 9 + 5 = 36
Calculate the average.
366 = 6
calculate the squared difference
(3 – 6)2 = 9
(5 – 6)2 = 1
(6 – 6)2 = 0
(8 – 6)2 = 4
(9 – 6)2 = 9
(5 – 6)2 = 1
Add all the squared differences together.
9 + 1 + 0 + 4 + 9 + 1 = 24
Calculation results
The population variance is
246 = 4
The sample variance is
246 – 1 = 4.8
What is standard deviation?
The square root of the variance is called the standard deviation, represented by σ. The standard deviation can reflect the dispersion of a data set. Two sets of data with the same mean do not necessarily have the same standard deviation.
Similarly, the standard deviation is also divided into population standard deviation and sample standard deviation.
The population standard deviation formula is
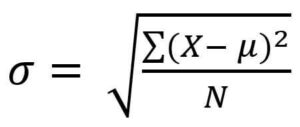 The sample standard deviation formula is
The sample standard deviation formula is
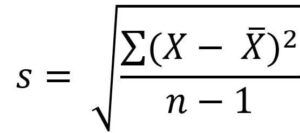
How to calculate standard deviation?
The standard deviation is the square root of the variance, so in addition to all the steps of computing the variance, there is an extra step, which is computing the square root of the variance.
In the above example, the data set is [3, 5, 6, 8, 9, 5]. We have calculated their variance. The population variance is 4 and the sample variance is 4.8.
So, the population standard deviation is
√4 = 2
The sample standard deviation is
√4.8 = 2.19
How to use the variance and standard deviation calculator
Using the calculator is simple, follow these 2 steps:
- Enter numbers in the input box. Separate each number with a comma or newline.
- Click Calculate button to calculate the variance and standard deviation of input numbers, or click Reset button to start a new calculation.
In the above example, just enter 3, 5, 6, 8, 9, 5 in the input box and then click calculate button. As shown in the figure, the calculation results are consistent with the above manual calculation.
![Variance and Standard Deviation of data [3, 5, 6, 8, 9, 5]](https://mathbz.com/wp-content/uploads/2022/09/Variance-and-Standard-Deviation-of-data-3-5-6-8-9-5.jpg)
Latest Calculators
Standard Form to Slope-Intercept Form Calculator
Slope Intercept Form Calculator
Slope Calculator: Calculate Slope, X-Intercept, Y-Intercept
Reciprocal of Complex Number Calculator
Conjugate Complex Number Calculator
Modulus of Complex Number Calculator
Profit Percentage Calculator: Calculate Your Profitability Easily
Attendance and Absence Percentage Calculator
Latest Checkers
Check if the given number is an almost perfect number.