Unusual Number Checker

Check if the given number is an unusual number.

Have you ever come across a number that stands out from the rest? Unusual numbers are fascinating mathematical entities that possess a unique characteristic. In this article, we will explore the concept of unusual numbers, learn how to identify them using an efficient checker, and provide step-by-step instructions on its usage. Come join us on this exciting journey of uncovering the extraordinary.

Unusual Number Checker

Eg, Is 120 an Unusual Number? Enter 120 into the input box and click Check button.

Check Reset

What is an Unusual Number

An unusual number is a positive integer that has the distinct property of having a largest prime factor greater than the square root of the number itself. In other words, no matter how large the number is, its largest prime factor will always exceed the square root of the number. The formula to determine whether a number is unusual involves finding its prime factors and comparing the largest prime factor with the square root of the number.

For example, let’s consider the number 42. The square root of 42 is approximately 6.48. The prime factors of 42 are 2, 3, and 7. Among these factors, the largest prime factor is 7. Since 7 is greater than the square root of 42, which is 6.48, we can conclude that 42 is an unusual number.

In contrast, let’s take the number 15. The square root of 15 is approximately 3.87. The prime factors of 15 are 3 and 5. The largest prime factor is 5, which is not greater than the square root of 15. Therefore, 15 is not considered an unusual number.

By comparing the largest prime factor with the square root of a number, we can determine whether it falls into the category of unusual numbers.

What is Unusual Number Checker

The unusual number checker is a powerful tool designed to quickly determine whether a given number is unusual. It saves time and effort by automating the process of finding prime factors and comparing them with the square root of the number. With just a few clicks, you can uncover the uniqueness hidden within any number.

How to Use the Unusual Number Checker

Follow these simple steps to use the unusual number checker:

1Enter the number you want to check in the designated input field.
2Click the Check button to initiate the verification process.
3Click the Reset button to start a new verification.

The checker will quickly analyze the number and display the result.

If the number is determined to be unusual, the checker will provide a confirmation message. If not, it will indicate that the number is not unusual.

Solved Examples by the Unusual Number Checker

Let’s explore a couple of examples to illustrate how the unusual number checker works:

Example 1:

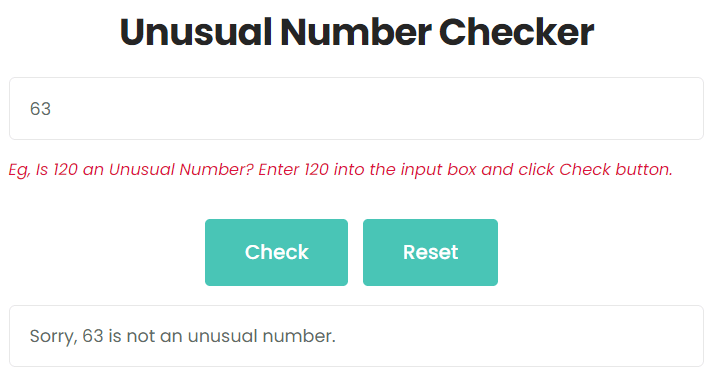
Is 63 an unusual number?

Enter 63 into the input box and click Check button. As shown in the figure, 63 is not an unusual number.

The square root of 63 is approximately 7.94. The prime factors of 63 are 3 and 7. The largest prime factor is 7, which is not greater than the square root of 63.

So, The number 63 is not classified as an unusual number.

Example 2:

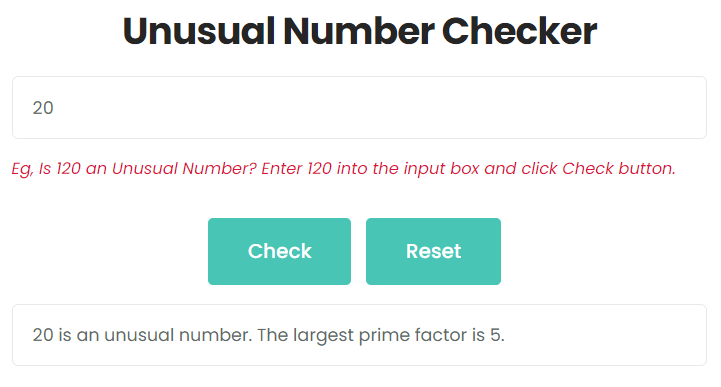
Checking if 20 is an unusual number?

Enter 20 into the input box and click Check button, as shown in the figure, 20 is an unusual number.

The square root of 20 is approximately 4.47. The prime factors of 20 are 2 and 5. The largest prime factor is 5, which is greater than the square root of 20.

So, the number 20 is determined to be unusual number.

First 100 Unusual Numbers

FAQS

Q1: What are prime factors?
A: Prime factors are the prime numbers that can divide a given number evenly without leaving a remainder.

Q2: Can unusual numbers be negative or fractional?
A: No, unusual numbers are defined as positive integers, so they cannot be negative or fractional.

Q3: Are there any known patterns or formulas to generate unusual numbers?
A: Unusual numbers do not follow specific patterns or formulas. They occur sporadically and require individual analysis.

Q4: Can unusual numbers be prime numbers?
A: Yes, unusual numbers can also be prime numbers. A prime number with a largest prime factor greater than its square root qualifies as an unusual number.

Q5: Do unusual numbers have any practical applications?
A: Unusual numbers are primarily studied in number theory and mathematics. While they may not have direct practical applications, their properties contribute to the broader understanding of numbers.