Triangle Height Calculator

In this article, we delve into the purpose of calculating the height of a triangle, explore the concept of triangle height, and unveil a variety of methods and techniques to compute it accurately. Whether you’re a student mastering geometry or a professional in architecture or engineering, understanding how to calculate the height of a triangle is an essential skill.

Triangle Height Calculator Calculator

Calculate Reset

What is Triangle Height

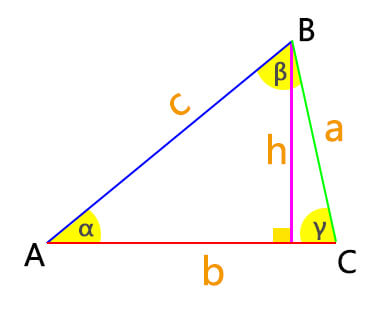
Before we dive into the methods, let’s establish what we mean by “triangle height“. The height of a triangle is the perpendicular distance from a base to the opposite vertex. It’s like measuring how tall the triangle stands within the two-dimensional plane it occupies.

How to Calculate Triangle Height (Multiple Methods)

Calculating the height of a triangle is a versatile skill, and you have a toolkit of techniques at your disposal. Here are several methods to calculate the height of a triangle:

Method 1: Base and Area Method

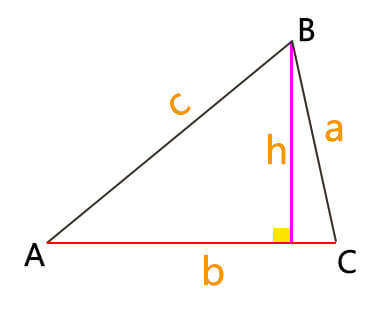Measure the length of the base of the triangle (Base).

Measure the area of the triangle (Area).

Use the formula:

height = 2 * areabase

Example: Imagine you have a triangle with a base of 10 inches and an area of 30 square inches.

Height = 2 * 30 square inches10 inches

Height = 6 inches

The height of your triangle is 6 inches.

Method 2: Side and Angle Method

Measure one side of the triangle (Side).

Measure the angle formed between this side and the height you want to find (Angle).

Use the formula:

Height = Side * sin(Angle)

Example: You have a triangle with a side length of 8 cm, and you want to find the height corresponding to a 60-degree angle.

Height = 8 cm * sin(60°)

Height = 6.93 cm

The height of your triangle is approximately 6.93 cm.

Method 3: SSS (Side-Side-Side):

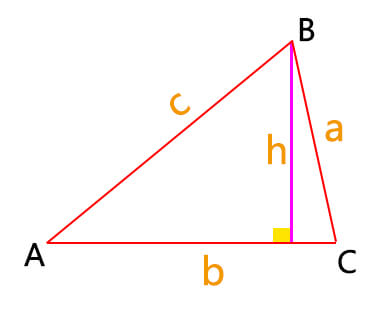The SSS method doesn’t directly provide the height of the triangle, but it can be used in conjunction with other methods to calculate the height. Here’s how to incorporate it:

Measure all three side lengths of the triangle (Side 1, Side 2, and Side 3).

Determine the semi-perimeter (s) using the formula:

S = (Side1 + Side2 + Side3)2

Use Heron’s Formula to calculate the area of the triangle:

A = √(s * (s – Side1) * (s – Side2) * (s – Side3))

Once you have the area, you can calculate the height using the formula:

height = 2 * A/base

In this case, the base can be any of the three sides.

Example: Consider a triangle with side lengths: 3, 4 and 5. Calculate the height of the triangle.

First, calculatethe semi-perimeter of the triangle

S = (Side1 + Side2 + Side3)2

S = (3 + 4 + 5)2 = 12/2 = 6

Second, calculate the area of the triangle using Heron’s formula:

A = √(s * (s – Side1) * (s – Side2) * (s – Side3))

A = √(6 * (6 – 3) * (6 – 4) * (6 – 5)) = √(6 * 3 * 2 * 1) = 6

Now that we have the area (A=6), we can use the formula for the area of a triangle:

Area = Base * Height2

to find the height. Rearrange the formula to solve for the height:

Height = 2 * AreaBase

Height = 2 * 64 = 124 = 3

So, the height of the triangle is 3 units, It’s a right triangle.

Method 4: AAS (Angle-Angle-Side):

With the AAS method, you have information about two angles and one side length that is not included between them. Here’s how to proceed:

Measure two angles of the triangle (Angle A and Angle B).

Measure a side length (Side c), but this side should not be between the two given angles.

Calculate the third angle (Angle C) using the fact that the sum of angles in a triangle is 180 degrees.

Determine the height using the formula:

Height = Side_c * sin(Angle A)

FAQs

Q: What is the height of a triangle?
A: The height of a triangle is the perpendicular distance from a base to the opposite vertex, measuring how tall the triangle stands within a 2D plane.

Q: Why is it important to calculate the height of a triangle?
A: Calculating the height is crucial in geometry, construction, engineering, and various applications where accurate measurements are essential.

Q: What is the base and area method, and when is it used?
A: This method uses the base length and area of the triangle to find the height. It’s applicable when you have these measurements available.

Q: What is the side and angle method, and when is it used?
A: This method calculates the height using a side length and the angle between that side and the height. It’s useful when you know a side length and the corresponding angle.

Q: Can the height of any type of triangle be calculated using these methods?
A: Yes, these methods can be applied to various types of triangles, including right triangles, scalene triangles, isosceles triangles, and equilateral triangles.

Q: Are these methods suitable for both acute and obtuse triangles?
A: Yes, the methods are applicable to triangles of all types, including acute, obtuse, and right triangles.

Q: Is there a method that's considered the most accurate for calculating triangle height?
A: The choice of method depends on the available data and specific triangle properties. All methods are accurate when applied correctly.

Q: Are there online calculators or tools available for calculating triangle height?
A: Yes, there are online calculators and software tools that can simplify the process of calculating triangle height based on the given data.Like the triangle height calculator provided on this page.