Triangle Area Calculator

6 Methods for Precise Calculation

In the realm of geometry, one often finds themselves on a quest to measure the space within a triangle. This is where the Triangle Area Calculator steps in as your trusty guide. This article aims to shed light on the calculator’s purpose, explore the concept of triangle area, and unveil a treasure trove of methods to calculate it. Be prepared to embark on a journey through six distinct techniques, each designed to help you conquer the challenge of finding the area of a triangle.

Triangle Area Calculator

Calculate Reset

What is Triangle Area

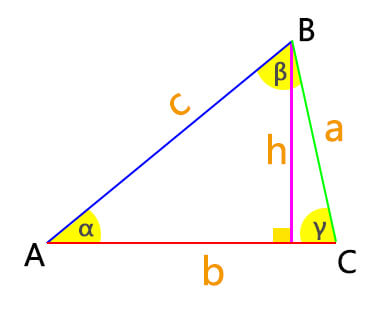
Before diving into the calculations, let’s clarify what we mean by “triangle area“. The area of a triangle is the amount of space enclosed within its three sides. It’s akin to measuring the space occupied by the triangle on a two-dimensional plane.

How to Calculate the Triangle Area

Calculating the area of a triangle is an art, and you have a palette of techniques at your disposal. Here are six different methods to compute the area of a triangle:

Method 1: Side and Height (Base and Height)

Measure the length of one side of the triangle (the base).

Measure the perpendicular distance from the base to the opposite vertex (the height).

Apply the formula:

Area = 12 * Base * Height

Example: Imagine you have a triangle with a base of 8 inches and a height of 6 inches.

Area = 12 * Base * Height

Area = Area = 12 * 8 inches * 6 inches

Area = 24 square inches

The area of your triangle is 24 square inches.

Method 2: SSS (Side-Side-Side)

In this method, you have information about all three side lengths of the triangle, and you can use the Heron’s Formula to calculate the area. Heron’s Formula states that the area (A) of a triangle with sides of lengths a, b, and c and semi-perimeter (s) is given by:

A = √(s (s – a) (s – b) (s – c))

Where:

s is the semi-perimeter, calculated as a + b + c2.

Method 3: ASA (Angle-Side-Angle)

To use this method, you need to know two angles and the side length between them. Here are the steps:

Measure two angles of the triangle (Angle A and Angle B).

Measure the length of the side between the two given angles (Side c).

Calculate the third angle (Angle C) using the fact that the sum of angles in a triangle is 180 degrees.

Calculate the height of a triangle using the formula

h = c * sin(A)

Calculate the base of a triangle using the Law of Sines

b = c * sin(B)sin(C)

When the base and height are known, we can easily calculate the area of the triangle. (see method 1)

The final formula is

A = c² * sin(A) * sin(B)2sin(C)

Where

A, B, and C represent the three interior angles of the triangle.
c represents the side opposite angle C.

Method 4: SAS (Side-Angle-Side)

With this method, you have information about two side lengths and the included angle. Here’s how to calculate the area:

Measure two side lengths of the triangle (Side a and Side b).

Measure the included angle (Angle C) between the two given sides.

Use the formula:

A = 12 * a * b * sin(C)

Where

C is the included angle, and
sin(C) is the sine of Angle C.
a and b represent two side lengths of the triangle

Method 5: SSA (Side-Side-Angle)

In the SSA method, you know two side lengths and an angle not included between them. This method is less reliable as it can lead to two different triangle configurations or no triangle at all.

Measure two side lengths of the triangle (Side a and Side b).

Measure an angle (Angle A), but this angle should not be between the two given sides.

Use the law of sines to find the angle B.

B = arcsin(b * sin(A)a)

Calculate the angle C using the fact that the sum of angles in a triangle is 180 degrees.

C = 180 – A – B

When all the angles of the triangle are known, you can use Method 3 (ASA) or Method 4 (SAS) to calculate the area of the triangle.

Method 6: AAS (Angle-Angle-Side)

In the AAS method, you have information about two angles and one side length that is not included between them. Here’s how to proceed:

Measure two angles of the triangle (Angle A and Angle B).

Measure a side length (Side c), but this side should not be between the two given angles.

Calculate the third angle (Angle C) using the fact that the sum of angles in a triangle is 180 degrees. (Just like method 5 mentioned)

Determine the area using the formula based on the ASA method (method 3) as explained earlier.

FAQs

Q: What is the area of a triangle?
A: The area of a triangle is the measure of the space enclosed within its three sides.

Q: Why is it important to calculate the area of a triangle?
A: Calculating the area is essential for various applications, including geometry, architecture, and engineering.

Q: How many methods are there to calculate the area of a triangle?
A: There are six primary methods: base and height, SSS, ASA, SAS, SSA, and AAS.

Q: What is the side and height method, and when is it used?
A: This method involves using the base and height of a triangle to calculate the area and is applicable when you know one side and the perpendicular height.

Q: What are the other methods, and when are they used?
A: SSS, ASA, SAS, SSA, and AAS methods are used when you have specific combinations of side lengths and angles, requiring trigonometric principles for area calculation.

Q: Are these methods suitable for all types of triangles?
A: Yes, these methods can be applied to various types of triangles, including scalene, isosceles, and equilateral triangles.

Q: Do I need special tools to calculate the area of a triangle?
A: No, you can perform these calculations with basic measuring tools and mathematical principles.

Q: Which method is the most accurate for calculating triangle area?
A: The accuracy of each method depends on the data available and the specific triangle. All methods are accurate when applied correctly.

Q: Why is it essential to learn multiple methods for calculating triangle area?
A: Learning multiple methods allows you to tackle various scenarios and types of triangles, enhancing your problem-solving skills in geometry.