Trapezoid Calculator for Perimeter, Area and Height

Welcome to the world of precise geometry with the Trapezoid Calculator. This versatile tool is designed to simplify the calculations associated with trapezoids, enabling you to effortlessly determine perimeter, area, and height.

Trapezoid Calculator

Calculate Reset

Definition

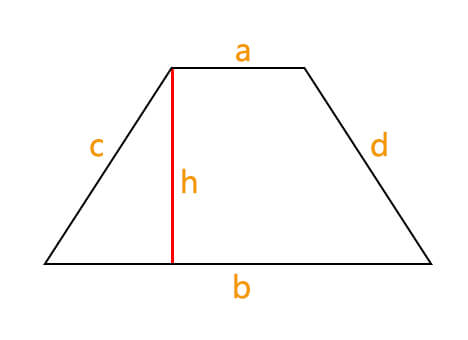A trapezoid is a quadrilateral with at least one pair of parallel sides. These parallel sides are called the bases (a and b), while the non-parallel sides are the legs (c and d). The height of a trapezoid is the perpendicular distance between the bases (h).

How to Calculate the Trapezoid Perimeter

Calculating the perimeter of a trapezoid involves adding the lengths of all its sides. Here’s a step-by-step guide:

Identify the lengths of the bases (a and b) and the lengths of the legs (c and d).

Add the lengths of all sides:

Perimeter = a + b + c + d

Example: If base a is 8 units, base b is 12 units, leg c is 5 units, and leg d is 7 units, the perimeter is

Perimeter = a + b + c + d = 8 + 12 + 5 + 7 = 32 units

How to Calculate the Trapezoid Area

Determining the area of a trapezoid involves a straightforward formula:

Identify the lengths of the bases (a and b) and the height (h).

Use the formula

Area = 1/2 * (a+b) * h

Example: If base a is 8 units, base b is 12 units, and the height h is 6 units, the area is

Area = 1/2 * (a + b) * h = 1/2 * (8+12) * 6 = 60 square units

How to Calculate the Trapezoid Height

Finding the height of a trapezoid involves rearranging the area formula:

Identify the lengths of the bases (a and b) and the area (A).

Rearrange the formula to solve for the height:

h = 2A/ (a+b)

Example: If base a is 8 units, base b is 12 units, and the area A is 60 square units, the height

h = 2A / (a + b) = 2 * 60 / (8 + 12) = 6 units

FAQs

Q: What is a trapezoid?
A: A trapezoid is a quadrilateral with at least one pair of parallel sides. The parallel sides are called the bases, and the non-parallel sides are the legs.

Q: How does the Trapezoid Calculator work?
A: The Trapezoid Calculator computes various parameters, including perimeter, area, and height, based on the input values provided, such as the lengths of the bases and legs.

Q: Is a trapezoid the same as a parallelogram?
A: No, a trapezoid has only one pair of parallel sides, while a parallelogram has two pairs of parallel sides.

Q: Can a trapezoid have equal angles?
A: Yes, a trapezoid can have equal angles, especially if it is an isosceles trapezoid where the non-parallel sides are of equal length.

Q: What is the height of a trapezoid?
A: The height (h) of a trapezoid is the perpendicular distance between the bases. It can be calculated using the area formula or by other geometric methods.

Q: Can a trapezoid have a right angle?
A: Yes, a trapezoid can have a right angle if one of the legs is perpendicular to both bases. Such a trapezoid is known as a right trapezoid.

Q: Are there different types of trapezoids?
A: Yes, trapezoids are classified based on the lengths of their sides. A trapezoid with equal-length legs is called an isosceles trapezoid.

Q: What are the applications of trapezoid calculations in real life?
A: Trapezoids are commonly encountered in architecture, engineering, and design. For example, the shape of some roofs and tables may be modeled as trapezoids.

Q: Can the Trapezoid Calculator handle irregular or non-convex trapezoids?
A: The calculator is designed for convex trapezoids. For irregular or non-convex shapes, the results may not be accurate.

Q: Is there a limit to the size of input values in the calculator?
A: The Trapezoid Calculator is designed to handle a wide range of input values, but extremely large or small values might result in numerical precision limitations.

Q: Can a trapezoid have bases of equal length?
A: No, by definition, a trapezoid has one pair of parallel sides (bases) of different lengths. If the bases are equal, it would be a parallelogram.

Q: Does the calculator round off results, and how many decimal places are provided?
A: The calculator provides results with high precision, accommodating six decimal places without rounding off.