Equal Symbol
2 + 2 = 4
What comes to your mind when you use this equation in your life? Of course, you take it as an equal sign. How is it possible to write that two integers are similar to one? It is possible with an equal sign that shows equality on both sides of the equation. Suppose there's not any specific sign to show equality not only in mathematics but in other subjects too. Is it fair then? Not at all; you come up with an imagination that refers to equality in the calculation but doesn't have any sign to present it in written form. In order to use this sign correctly, you need to understand what an equal sign is and its usage in mathematics. To answer the queries related to type on your PC or android, you need to follow specific steps accordingly.
There are multiple codes of the equal sign while working on the computer. The equal symbol shows the clarity that two things are exactly equal.
Apart from that, there are multiple variants of the equal sign, i.e. (≠), (≡), (==). We'll discuss all these in our article in order to let you deliver a better understanding of the equal symbol. Without further ado, let's discuss it in detail.
What is an equal sign?
Having discussed the importance and overview of the equal sign, let's learn what equal sign is.
It is a mathematical symbol to represent equality in a definite and well-versed manner. As far as its invention is concerned, credit goes to Robert Recorde. He invented this sign in 1557, as per record. In general terms, it shows equality of value between the two expressions and numbers. Apart from mathematics, it is used in other subjects to show the balance irrespective of the no. of integers.
For example: 1 + 3 + 5 = 9
If you analyze this equation, the integers on the left side are more than the right one; 3 on the left and one on the right sides. But, what makes them equal is the value. The total value of left-sided three integers is 9, equal to the right-sided integer value: 9.
Equal is derived from the "æqualis."
It is a Latin word which meaning is identical, uniform, or equal. This (=) sign became famous after being used in 1557. At some time, (II) was used by some people, then people adopted the current sign. The sign Robert Recorde used in his book in 1557 was much wider than the current one.
What is the meaning of the equal sign in mathematics?
Here comes the meaning of the equal sign. Before further discussing, let's take an example.
x + 1 = 2, then it is understood that the value of x would be 1 to balance both sides; otherwise, you must not place the equal sign between these two expressions. If it's placed, then x has value 1. Apart from that, we can get the x value mathematically in that equation.
x = 2 - 1
x = 1
This is how we can calculate the exact value of any alphabet whose value is not given. If values are equal on both sides, then we use an equal side between them. Sometimes you may have seen the approximate sign (≈). It's due to the minor difference in values that you cannot ignore. For example, 1.999 ≈ 2
Sometimes this difference is ignored knowingly in mathematics when you deal with a large value; this is when the equal sign is used for own feasibility.
We have discussed the equal sign in equations. It is used in measurement too. For example, if you measured a specific body height, length, and width. Now, if you want to measure the volume of that body, then it will be written as follows:
Volume = height × length × width
suppose height = 10m, length = 5m and width 2m
Volume = 10 × 5 × 2
Volume = 100 cubic meter
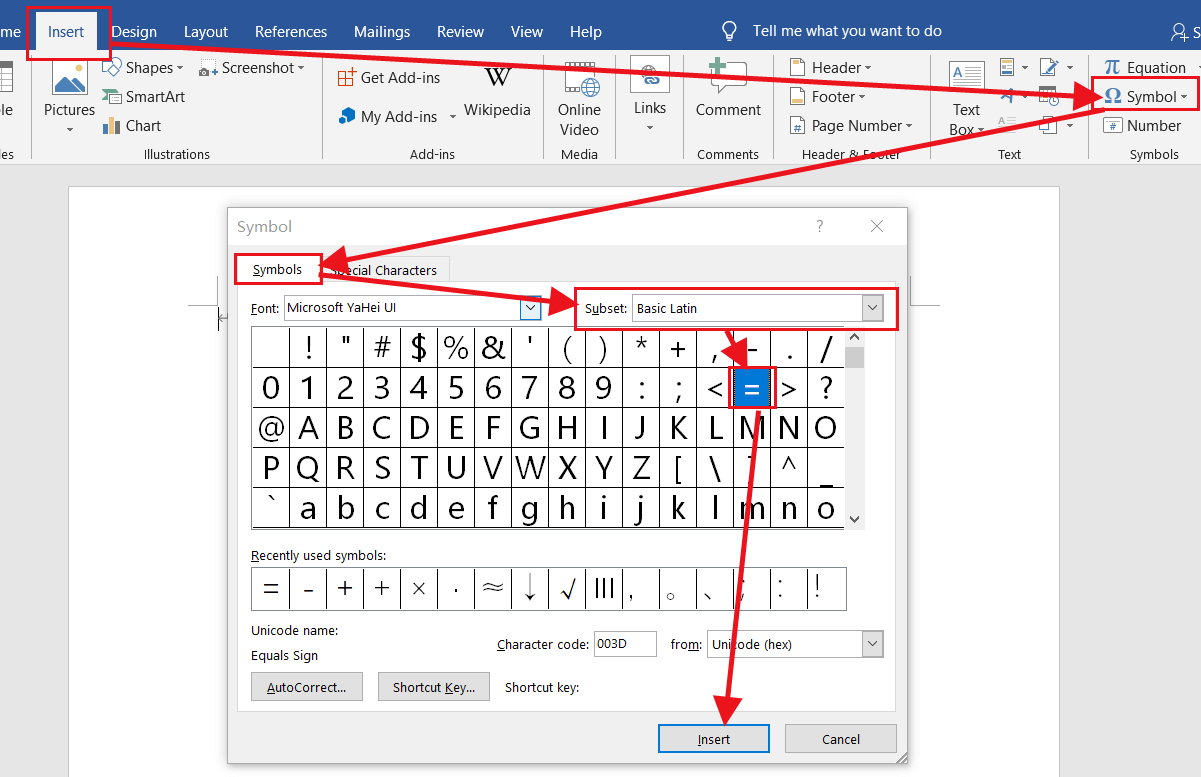
How to type an equal sign?
Type Equal Sign on Windows
In order to type equal sign on PC windows, you need to find the equal sign on the keyboard. As per your suitability, it is located on the left side of the BACKSPACE key. The (+) and (=) signs are placed on the same button. Just only press that key, then an equal sign will appear on your PC screen.
Type Equal Sign on Mac
Well, to type equal sign on MAC follows the same process which we follow for PC windows. If you're using an American keyboard, then an equal sign will be available on that keyboard. Click it, and you'll get an equal sign on your screen. Avoiding pressing SHIFT and equal sign; otherwise, the plus sign will appear instead.
Type Equal Sign on IPhone
Many IPhone users find difficulty in searching the equal sign to type on screen. Here is a series of steps you need to follow will land you to the equal sign.
- First, open keyboard.
- Press ?123 button on the down-left corner.
- Find the #+= button in the lower left corner and press it.
- Find the equal sign there and click on it.
Type Equal Sign on Android Phone
Do you find it difficult to type the equal sign on android? You need not worry at all. Follow the two steps given below and type it with ease in no time.
- First of all, open the android keyboard.
- Then go on the down-left corner and press on the "?123" button.
- You'll land with various symbols and keys there.
- Find the equal sign there and click on it.
- The equal sign will appear on your android screen.
Type Equal Sign in Word/Excel/PowerPoint
It is pretty easy to type equal sign on excel. Press the += button directly at the left side of BACKSPACE or follow the steps written below.
- Insert a new symbol from the insert menu.
- After pressing, you will see the symbol dialog.
- Browse the symbol (=) in mathematical operators and then insert it by clicking it.
Codes of Equal Sign
| Unicode | U+003D | |
|---|---|---|
| Alt Code | Alt 61 | |
| ASCII Code | 61 | |
| Hex Code | = | |
| HTML Code | = | |
| CSS Code | \003D | |
| HTML Entity | = |
Variants of the Equal Sign
There are variants of equal sign with slight differences. These variants are somehow related to equal sign with different meanings as given below:
Not Equal (≠)
This is a sign of not equal. It shows that the two terms are not equal. In mathematics, it represents inequality. In general, we can say that it is the opposite process of an equal symbol. If a clear value difference exists between two expressions, we can put it between them.
For example, 4+ 5 ≠ 45
It shows the clear difference between the values of both sides' integers. The left side integers value is 9, while the right-sided integer value is 45. There's a clear difference between them. This is where not equal sign is written between different values.
Triple Equal (≡)
It is named as a triple equal sign. A third bard is put on the equal sign. It shows the similarity in terms. In other words, when two terms are identical, then you can put a triple equal sign. It doesn't mean these terms/expressions have the same value. The third bar on the equal symbol in Unicode is the code point.
Double Equal (==)
It is called a double equal sign—it is a conditional sign of giving information to the computer.
For example, a == 9, then print a
It puts the conditions if equals to 9, then print it; otherwise, don't. In simple words, a double equal sign puts a condition to the test the values whether they are similar or not.
Approximately (≈)
This is a sign of approximately. If two values are almost the same but not exact, then this sign is used. When you talk about two expressions that are approximately equal to each other, this sign refers to this minor difference.
For example, 13 + 12.999 ≈ 26 (a minor difference exists between them)
Conclusion
The equal sign has great importance when it comes to equality. When it has been mentioned between the terms or expressions, it's understood either terms or integers (in math) have the same value. When there's a minor difference, then an approximately sign is put between the terms.
To type equal sign on PC widows, Android, IPhone, excel, and PowerPoint, you need to follow different steps for each one of them. Double equal signs or triple equal signs are the variants of equal signs (each one of these is discussed in this article).
There are codes for equal signs, i.e., Unicode, Alt code, ASCII, Hex code with different symbols. To use equal signs, it is a must to learn about it in detail.