Approximately Symbol

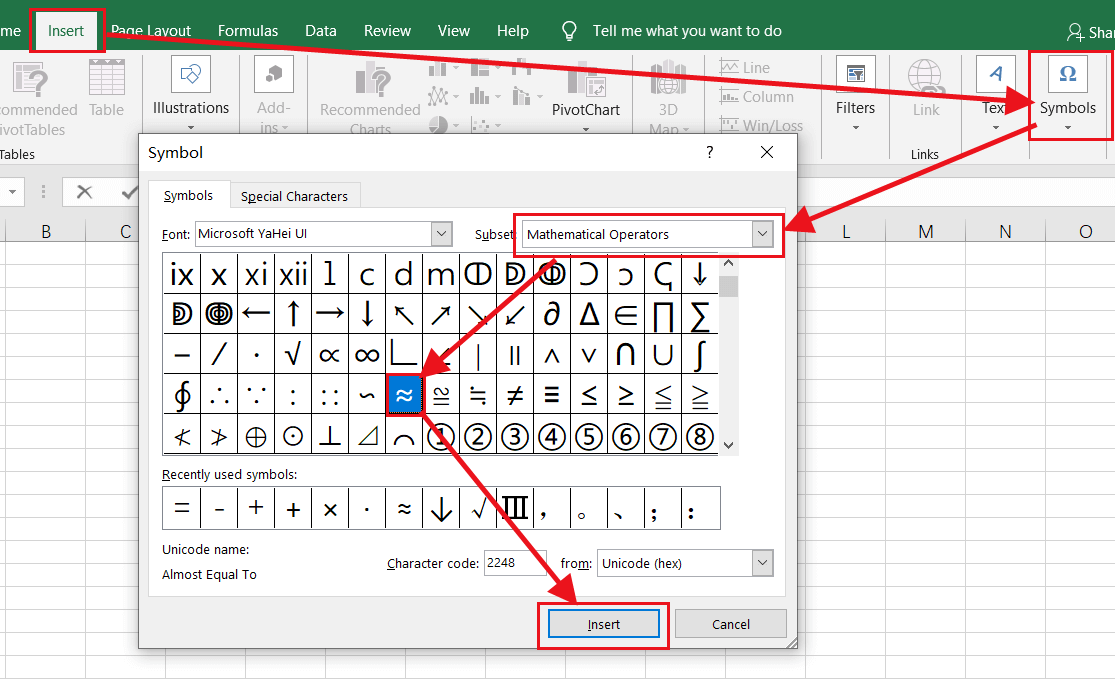
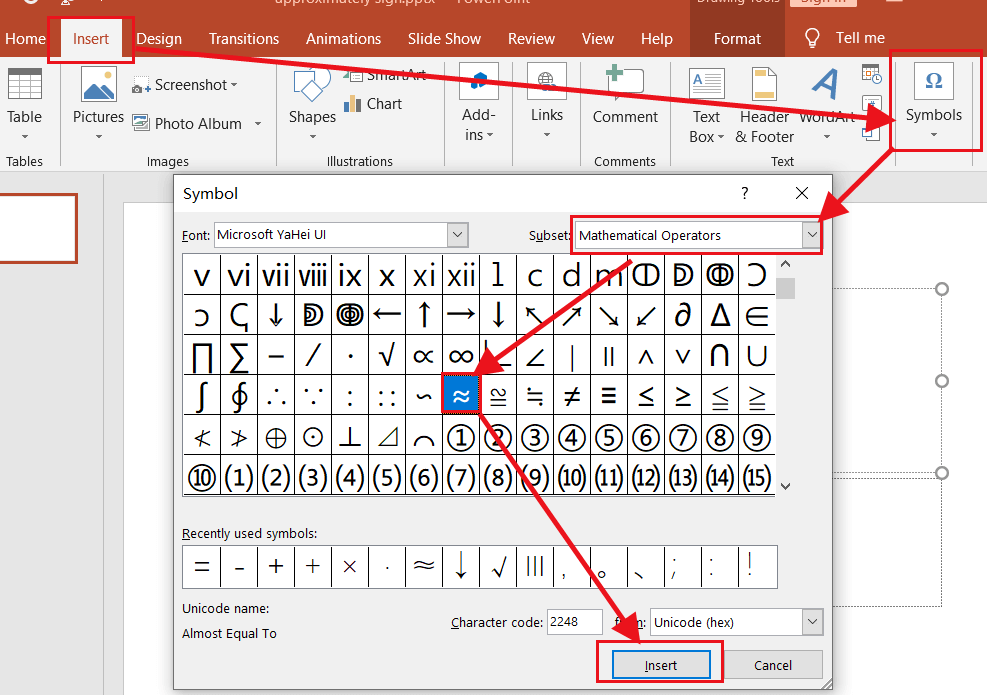
An approximate of something is what is logically similar to another thing but it is not equal to it. The word approximation has been taken from the Latin word "approximatus" which means "something which is very close, or near". Any word related to it like approximately and approximate (of something) are all used in technical or scientific terms. The sign for approximately is ≈.

An abbreviation of this word can also be used in its place which is "approx". Words like around or roughly are used in the same context as they have similar meaning. Apart from mathematics, it can be used to define other properties like an image or description. However, when it comes to mathematics, it is used for defining values and quantities which are closely related and similar but are not equal to each other.

Often, ≈ symbol is usually used to define digits and numbers but it is also applied to equations in mathematics to define certain functions and shapes etc. In other sense, a simpler way to understand it is that when a model is presented instead of an original one which is hard to use, then they are referred to as approximately equal to each other. It makes a calculation much easier. This symbol can also be used when the information is not complete and accurate representation is not available.

What is an approximately sign?

As it has been mentioned earlier that comparison of quantities is performed then their end values are sometimes not equal but are quite close or identical. In such cases it is irrational to use an equal sign that shows both quantities are parallel because they are similar not exactly parallel. Therefore the sign for approximation has a "≈" symbol which uses wavy lines, parallel to each other.

In this equation, the symbol denotes the fact that log of 4 is approximately equal to the digits that have the value of 0.477.

While using it in math, when the measurements of an angle is equal to another angle and their respective sides are quite similar in proportion, at that time the respective figures are said to be similar. For such figures, their approximation is denoted by this symbol.

How is approximately sign used in Math?

It is a symbol which is used in mathematics in order to indicate that two equations are similar to each other but not equal. For instance, take the example of constant e which is called as the Euler's number. It is similar or we can say approximately equal to the value of 2.718. So, their equation will be expressed as follows: e ≈ 2.718 There are many other values and digits which are required to represent this number but the use of approximation here enables to simplify its representation. It denotes that the values written on left are similar to the values written on right. This balances out the overall mathematical expression.

It helps in mathematics to deal with situations and equations where the exact number of digit is quite difficult or not easily obtained. But some of the known digits exist which can be used to represent the actual form. It helps in finding no significant deviation. It can also be used where the digit is irrational for instance, the digit pie π which is represented in short form of 3.14159.

Another use includes such expression where the values become larger than expected. It can be explained by an example of k. Its sum is (k/2) + (k/4) + (k/8) +…(k/2ⁿ) which is said to be approximately equal to k.

How can we use approximately sign in simple calculations?

In mathematics, we are sometimes facing situations where we have expressions which are not exact but rather an estimate. It leads to a stress in getting the real answer. So, estimation can be defined as the search of finding a digit which is closer to the exact answer.

It is not about getting the right answer but about getting an estimation which is good enough for the argument. For such places, this symbol is used to denote estimation. For example, a person says it will take about half an hour for them to reach home. It is estimation, not the correct amount of time.

Therefore while balancing out expressions, when figures are being compared, the symbol of approximately is used. A person measured two sides of a square; the remaining two are being estimated to be equal to a certain digit or angle. In such cases, he or she can use this symbol to stabilize their equation.

This method of approximation helps to save time for example take the simplest situation where a person wants to grow flowers in a row. The length of their row is 58.6 cm and the plants have to be planted at a distance of about 6 cm in length from each other.

How many flowers will be needed to be planted in that row? Now we use the concept of approximation by saying that as 58.6 is close enough to the digit 60 as 58.6 then by dividing 60 with 6 we get 10.

As by that statement we get the following approximation: 58.6 ≈ 60 Then, by using the approximation method of 58.6 ≈ 60 we get our answer to solve this problem.

The symbol of approximation can help solve the human errors we face while using a calculator. A person is trying to calculate 56 about 107 times. The answer the person gets on the calculator says 952.

Now, the question is, is the answer correct? Well, a person might think that the answer is not right because when 56 is taken 107 times then it is quite bigger than 100 times of 50 which makes it 5000.

So, that means a person might have put in some digit wrongly in to the calculator. Such estimations save from mistakes however mathematical expressions of such estimations are denoted by the symbol ≈ where the values are too large.

How to type an approximately symbol?

Type an Approximately Sign on Windows

1. Place the cursor at desired spot where the symbol is needed.
2. Open NumLock, and hold the Alt key on your board.
3. While holding it, press 41430.

Type an Approximately Sign on Mac

In order to type approximation symbol on a MAC book, the method which is used includes Option with X as Option + X.

1. Place the indicator where the symbol is required.
2. Press the Option and hold there.
3. While pressing Option, press the key X from keyboard.

Type an Approximately Sign in Word

Press 2248, then type ALT + x button at the same time. Or type the approximate sign by using ALT, press ALT + 8776. Or

1. Click on the Insert tab.
2. Click on the Symbol inside Insert tab.
3. Click on More symbols, then select "Mathematical Operators" subset
4. Click on the approximate symbol.

Type an Approximately Sign in Excel

Type the approximate sign by using ALT. Press ALT + 41430.

1. Click on the Insert tab.
2. Click on the Symbol inside Insert tab.
3. Click on More symbols, then select "Mathematical Operators" subset.
4. Click on the approximate symbol.

Type an Approximately Sign in Powerpoint

1. Click on the Insert tab.
2. Click on the Symbol inside Insert tab.
3. Click on More symbols, then select "Mathematical Operators" subset.
4. Click on the approximate symbol.

Codes of approximately sign

Difference between approximate variants ≈, ≅, ~ and ≃

For notations in math, there are some differences between the usage of various approximate signs and symbols. These include ≈, ≅, ∼ and ≃. They have slight difference between each other. All these symbols are related to the original approximate sign but they denote slightly different meanings.

Conclusion

Approximate symbol is used where the expressions are not equal to each other and are rather similar. These are used to denote the similarities between two expressions and not the equality. When the values are bigger and the differences become minor, the two expressions/values or two sides of an equation can be denoted by the symbol ≈.

In mathematical expressions this symbol is used to denote values of expressions whose values are not exactly known. There are many methods of inserting approximate symbols; however their codes can be used. It can be inserted in word, excel and power point the similar way but in order to add it onto a mac book, android and Iphone, there are other methods which should be used.

Variants of approximate symbol includes ≈, ≅, ~ and ≅ with slight differences among them. This symbol cannot be used as an equivalent for equal sign. Both of these signs have their own distinct properties for usage.