Sum of Squared Deviations Calculator

Calculate the Sum of Squared Deviations of dataset.

In the world of data analysis, understanding the variability and spread of data is crucial. One important measure of dispersion is the Sum of Squared Deviations. This powerful statistical tool allows us to analyze how individual data points deviate from the mean, providing valuable insights into the data’s distribution. In this article, we will delve into the Sum of Squared Deviations Calculator, exploring its definition, formula, and step-by-step calculation process.

Sum of Squared Deviations Calculator

Please enter numbers. Numbers separated by commas or new lines:

Eg, What is the SSD of a set of numbers 5, 10, 15 and 20? Enter 5, 10, 15, 20 into the input box and click Calculate button.

Calculate Reset

Understanding Variability

Before we delve into the nitty-gritty of the calculator, let’s grasp the concept of variability. In any dataset, variability refers to the differences or deviations of individual data points from the mean (average). A high variability indicates that the data points are spread out, while low variability suggests that the data points are close to the mean.

What is the Sum of Squared Deviations?

The Sum of Squared Deviations, also known as the Sum of Squares or SSD, is a statistical measure that helps us understand the dispersion of data points around the mean. It quantifies the total variability within a dataset by squaring each deviation from the mean and summing up these squared deviations.

You might wonder why we square the deviations instead of simply using absolute values. The reason lies in mathematics and statistical properties. Squaring the deviations not only ensures all values are positive but also penalizes larger deviations more significantly. This treatment provides us with valuable insights into the dataset’s overall dispersion.

Let’s break down the formula for the Sum of Squared Deviations (SSD):

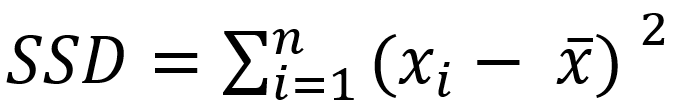
Sum of Squared Deviations formula

Where

SSD: Sum of Squared Deviations
Σ: Summation symbol (add up all values)
x_i: Individual data point
x: Mean of the dataset

How to Calculate the Sum of Squared Deviations

Calculating the SSD is a straightforward process that involves a few simple steps. Let’s walk through the process with a concrete example to solidify your understanding:

Find the Mean: Calculate the mean of the dataset by summing all the data points and dividing by the number of data points.
Calculate Deviations: Subtract the mean from each data point to find the deviation of each data point from the mean.
Square the Deviations: Square each deviation obtained in Step 2.
Sum the Squared Deviations: Add up all the squared deviations obtained in Step 3.

For example, Calculate the Sum of Squared Deviations for the dataset {5, 8, 10, 12, 15}.

Step 1: Calculate the Mean

Add all the data points:

5 + 8 + 10 + 12 + 15 = 50

Divide the sum by the number of data points:

50 / 5 = 10

Step 2: Calculate the Deviations

For each data point, subtract the mean:

5 – 10 = -5

8 – 10 = -2

10 – 10 = 0

12 – 10 = 2

15 – 10 = 5

Step 3: Calculate the Squared Deviations

Squared each deviations of dataset:

(-5)² = 25

(-2)² = 4

(0)² = 0

(2)² = 4

(5)² = 25

Step 4: Calculate the Sum of Squared Deviations

Add up all the squared deviations:

25 + 4 + 0 + 4 + 25 = 58

Therefore, the Sum of Squared Deviations for the given dataset is 58.

What is the Sum of Squared Deviations Calculator?

Our user-friendly Sum of Squared Deviations Calculator is a valuable tool designed to streamline the calculation process for data analysts, statisticians, and students alike. By simply inputting a dataset, the calculator automatically computes the Sum of Squared Deviations, saving time and effort in manual calculations.

How to Use the Calculator

Using the Sum of Squared Deviations Calculator is as easy as 1-2-3. Follow these simple steps to compute the SSD for your dataset:

1Enter your dataset into the calculator. Remember to separate each number with a comma or newline.
2Click the Calculate button, and the calculator will perform the SSD calculation for you.
3The calculator will display the sum of squared deviations, giving you a clear picture of the variability in your data. If you want to start a new calculation, please click the Reset button.

FAQs

Q: Can the SSD be negative?
A: No, the SSD is always a positive value as squared deviations are used.

Q: How is SSD different from variance?
A: The variance is the average of squared deviations, whereas the SSD is the sum of squared deviations.

Q: When is SSD used in data analysis?
A: SSD is used to analyze variability, identify outliers, and assess data quality.

Q: Is the Sum of Squared Deviations affected by outliers in the dataset?
A: Yes, the presence of outliers can significantly impact the SSD, as squared deviations amplify the effect of extreme values.

Q: Can SSD be used with any type of data, such as categorical or continuous variables?
A: SSD is most commonly used with continuous numerical data, but it can also be applied to categorical data if the categories can be numerically coded.

Q: What is the significance of SSD in regression analysis?
A: In regression analysis, SSD is used to determine the goodness of fit of the regression line to the data points.

Q: How can I interpret the value of SSD?
A: The value of SSD is a measure of the dispersion of data points around the mean. Smaller SSD values indicate less variability and tighter clustering around the mean.

Q: Can I use the Sum of Squared Deviations for comparing datasets of different sizes?
A: While you can use SSD for comparison, it’s essential to consider the sample size. Larger datasets may naturally have larger SSD values, so it’s better to use the coefficient of determination (R-squared) for meaningful comparisons.

Conclusion

The Sum of Squared Deviations Calculator is a valuable statistical tool that unlocks the secrets hidden within datasets. Armed with this knowledge, you can now embark on an exciting journey of data analysis, extracting meaningful insights from the vast sea of information. Embrace the power of the SSD calculator and gain confidence in your analytical prowess as you explore the fascinating world of statistics.

So, are you ready to unleash the potential of the Sum of Squared Deviations Calculator?

Sum of Squared Deviations Calculator