Sum of Multiples Calculator

Welcome to the sum of multiples calculator, this calculator is used to calculate the sum of all N multiples between A and B. Generally, to calculate the sum of multiples, several problems must be solved first:

1. Must understand what a multiple is? If an integer M is divisible by another integer N, then M is a multiple of another integer N.
2. Find the number of multiples within the specified range, such as: multiples of 7 from 1 to 100.
3. Add up the numbers found in the second step to get the result.

Obviously, these steps are too complicated for most people. So, the sum of multiples calculator is to simplify the above steps and let you get the answer easily. Of course, in addition to calculating the sum, there are other problems that will be solved by the sum of multiples calculator:

• How many multiples of N lying between A and B?
• What are the multiples of N between A to B?
• What is the smallest multiple of N between A and B?
• What is the largest multiple of N between A and B?
• What is the average of multiple of N between A and B?

If you want to calculate the sum of first N multiples M, please click here.

The multiples of 7 between 1 to 100 are

7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98

So, sum of their is

7 + 14 + 21 + 28 + 35 + 42 + 49 + 56 + 63 + 70 + 77 + 84 + 91 + 98 = 735

Use the sum of multiples calculator to calculate the sum of the multiples of 7 from 1 to 100.

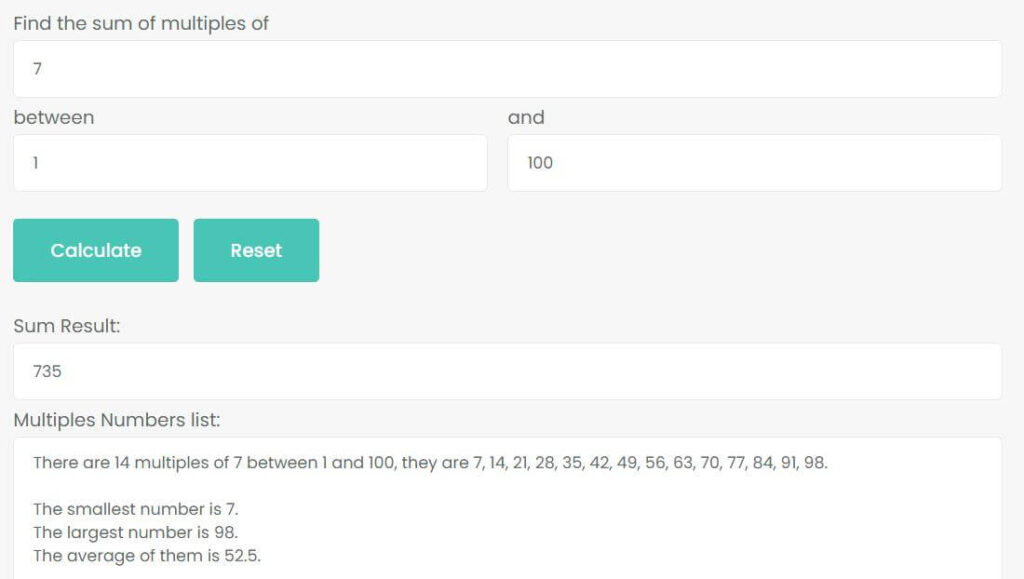Thus, there are 14 multiples of 7 between 1 and 100, and their sum is 735. The smallest number is 7, the largest number is 98. Their average  is 52.5.

The multiples of 9 between 300 to 700 are

306, 315, 324, 333, 342, 351, 360, 369, 378, 387, 396, 405, 414, 423, 432, 441, 450, 459, 468, 477, 486, 495, 504, 513, 522, 531, 540, 549, 558, 567, 576, 585, 594, 603, 612, 621, 630, 639, 648, 657, 666, 675, 684, 693.

So, sum of their is

306 + 315 + 324 + 333 + 342 + 351 + 360 + 369 + 378 + 387 + 396 + 405 + 414 + 423 + 432 + 441 + 450 + 459 + 468 + 477 + 486 + 495 + 504 + 513 + 522 + 531 + 540 + 549 + 558 + 567 + 576 + 585 + 594 + 603 + 612 + 621 + 630 + 639 + 648 + 657 + 666 + 675 + 684 + 693 = 21978

Use the sum of multiples calculator to find the sum of all multiples of 9 lying between 300 and 700.

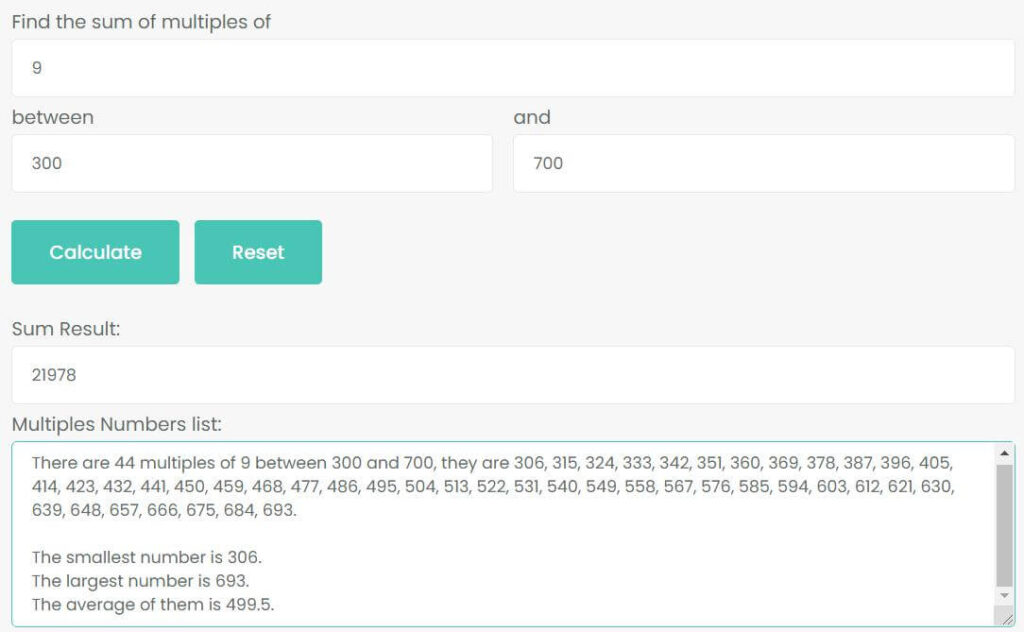Thus, there are 44 multiples of 9 between 300 and 700, and their sum is 21978. The smallest number is 306, the largest number is 693. The average of them is 499.5.

That’s all, make a try now.