Sum of Fractions Calculator

As we all know, the addition of fractions is not the same as the addition of integers. You cannot add two fractions directly. It is necessary to consider whether the denominators are the same. If the denominators are not the same, first convert the denominator to the same number. When the denominator changes, the numerator also changes accordingly. Therefore, a free online sum of fractions calculator is necessary.

Sum of Fractions Calculator

Calculate Reset

Solved examples using sum of fractions calculator

Same denominator

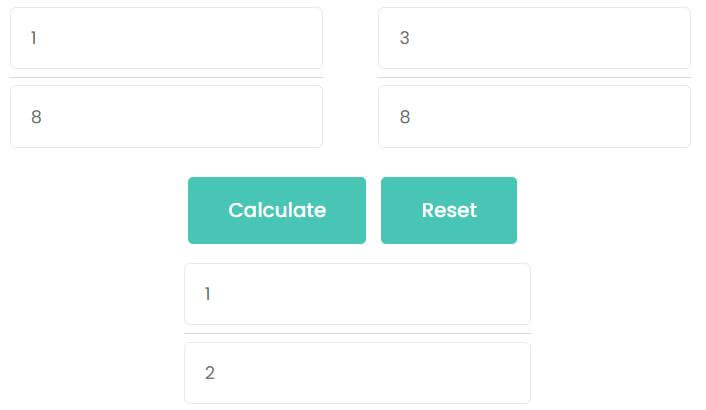
For example 1/8 + 3/8

Input 1 in the first numerator input box.
Input 8 in the first denominator input box.
Input 3 in the second numerator input box.
Input 8 in the second denominator input box.

1/8 + 3/8
= 4/8
= 1/2

Same denominator

Different denominators

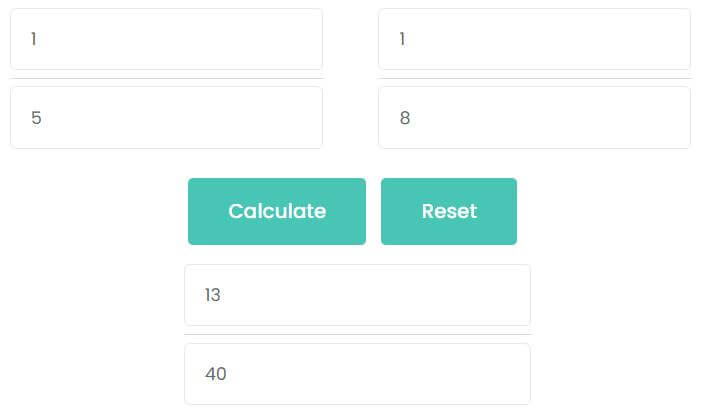
For example 1/5 + 1/8

Input 1 in the first numerator input box.
Input 5 in the first denominator input box.
Input 1 in the second numerator input box.
Input 8 in the second denominator input box.

1/5 + 1/8

= 8/40 + 5/40

= 13/40

Different denominators

Proper fraction plus improper fraction

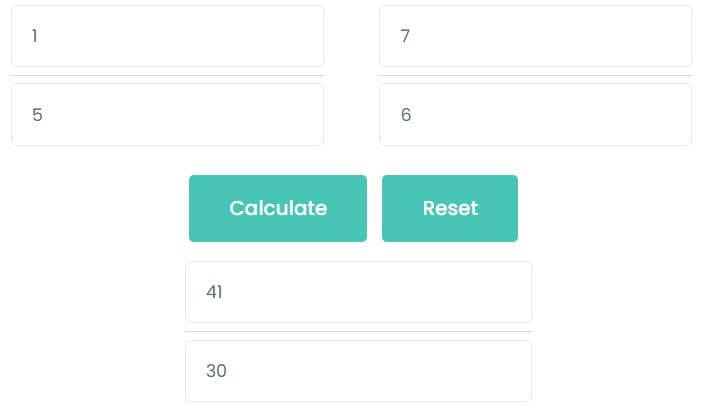
For example 1/5 + 7/6

Input 1 in the first numerator input box.
Input 5 in the first denominator input box.
Input 7 in the second numerator input box.
Input 6 in the second denominator input box.

1/5 + 7/6

= 6/30 + 35/30

= 41/30

Proper fraction plus improper fraction

Improper fraction plus improper fraction

3/2 + 8/5

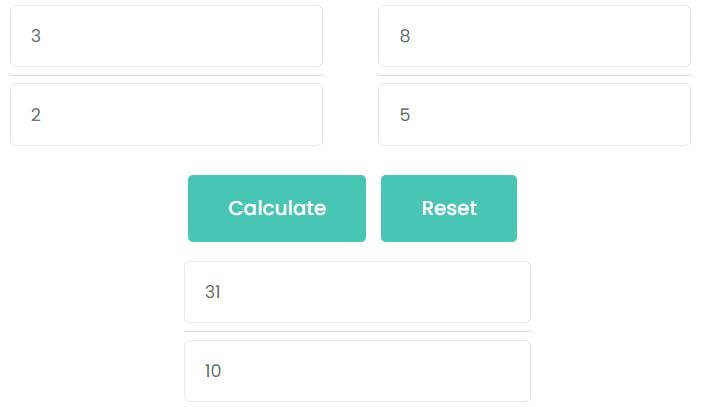
For example 3/2 + 8/5

Input 3 in the first numerator input box.
Input 2 in the first denominator input box.
Input 8 in the second numerator input box.
Input 5 in the second denominator input box.

3/2 + 8/5

= 15/10 + 16/10

= 31/10

Improper fraction plus improper fraction

Back to top of page