Sum of First N Multiples Calculator

Welcome to the sum of first N multiples calculator, as the name suggests, this calculator is used to calculate the sum of first N multiples M. For example, find the sum of first 15 multiples of 8. In here, N stands for 15, M stands for 8.

Obviously, the sum of first N multiples calculator needs to enter two parts of information: one is the exact number of the first N, and the other is the value of the multiple. Like the example above, just input 15 into the first input box and 8 into the second input box, then click calculate button.

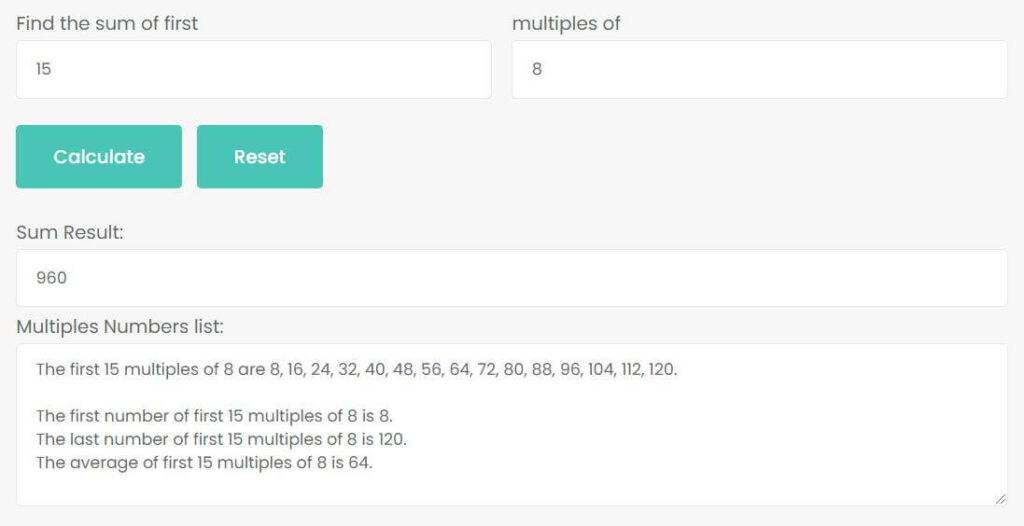As you can see, in addition to calculating the sum of first 15 multiples of 8, there is also a multiples numbers list, which will list all the numbers in the first 15 multiples of 8. At the same time, their average value will also be calculated. Therefore, the following problems can be easily solved:

• What is the sum of the first 15 multiples of 8?
• What are all the numbers in the first 15 multiples of 8?
• What is the first number of first 15 multiples of 8?
• What is the last number of first 15 multiples of 8?
• What is the average of first 15 multiples of 8?

Of course, if you are not calculating the sum of first N multiples, but calculating the sum of multiples in a range, you can use the sum of multiples calculator between A and B.

The first 8 multiples of 3 are

3, 6, 9, 12, 15, 18, 21, 24

So, sum of their is

3 + 6 + 9 + 12 + 15 + 18 + 21 + 24 = 108

Use the sum of first N multiples calculator to calculate the sum of first 8 multiples of 3.

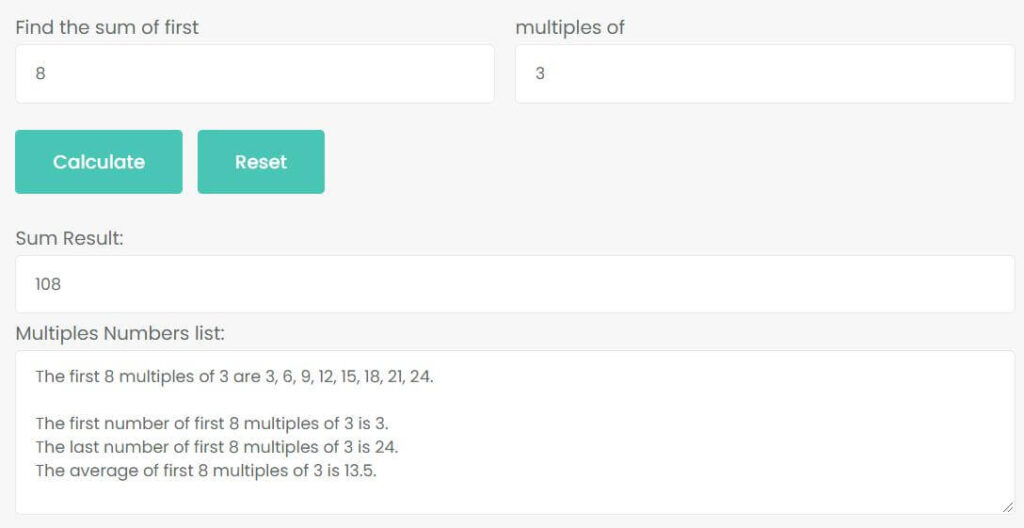Thus, the sum of first 8 multiples of 3 is 108. The first number is 3, the last number is 24. The average of first 8 multiples of 3 is 13.5.

The first 10 multiples of 6 are

6, 12, 18, 24, 30, 36, 42, 48, 54, 60

So, sum of their is

6 + 12 + 18 + 24 + 30 + 36 + 42 + 48 + 54 + 60 = 330

Use the sum of first N multiples calculator to calculate the sum of first 10 multiples of 6.

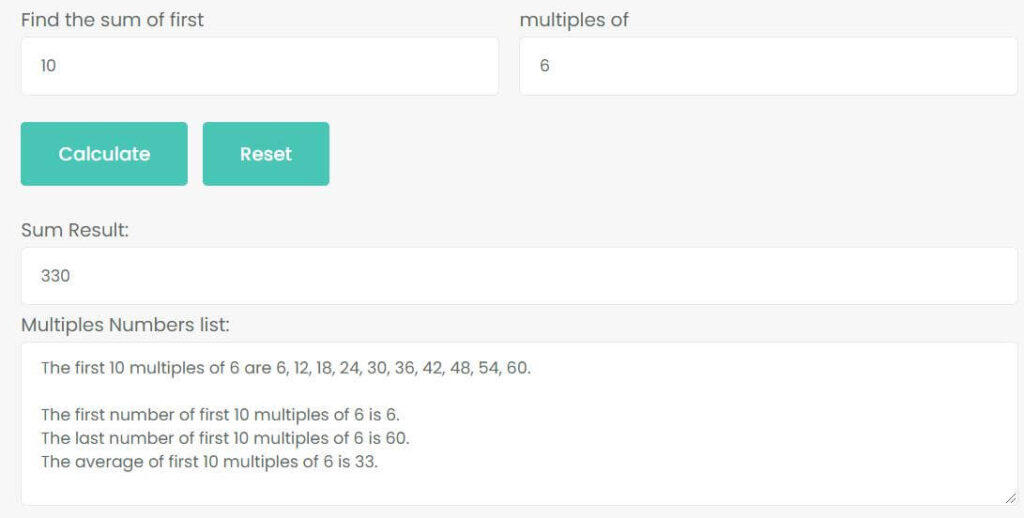Thus, the sum of first 10 multiples of 6 is 330. The first number is 6, the last number is 60. The average of first 10 multiples of 6 is 33.

Okay, now it is your turn.