Sum and Difference of Two Cubes Calculator with Steps

Welcome to the sum and difference of two cubes calculator with steps, this is a free online calculator. What information can be seen from the name of this calculator? Yes, it contains at least 4 parts:

1. This calculator is based on 2 cubes;
2. The calculator will calculate the sum of two cubes;
3. The calculator will calculate the difference of two cubes;
4. The calculation process will show detailed steps.

Is it the same as you think? Now, let’s take a look at the real face of the calculator.

As you can see, the use of the sum and difference of two cubes calculator is very simple, just enter two numbers and click calculate button. The calculator will calculate the sum of two cubes and the difference of two cubes at the speed of lightning. In addition, the calculation steps are displayed to meet special requirements.

Of course, the calculation steps are inseparable from the calculation formulas. The sum and difference of two cubes formulas are given below

Sum of two cubes formula

x³ + y³ = (x + y) * (x² – x * y + y²)

Difference of two cubes formula

x³ -y³ = (x – y) * (x² + x * y + y²)

Among them, x and y in the formula represent the two numbers to be input by this calculator. There is no doubt that the sum and difference of two cubes calculator will save you a lot of time.

Calculate using formula, the sum of the cubes 10 and 15 is

10³ + 15³
= (10 + 15) * (10² – 10 * 15 + 15²)
= 25 * (100 – 150 + 225)
= 25 * 175
= 4375

The difference of two cubes 10 and 15 is

10³ – 15³
= (10 – 15) * (10² + 10 * 15 + 15²)
= -5 * (100 + 150 + 225)
= -5 * 475
= -2375

Use the sum and difference of two cubes calculator to calculate the sum and difference of the cubes 10 and 15.

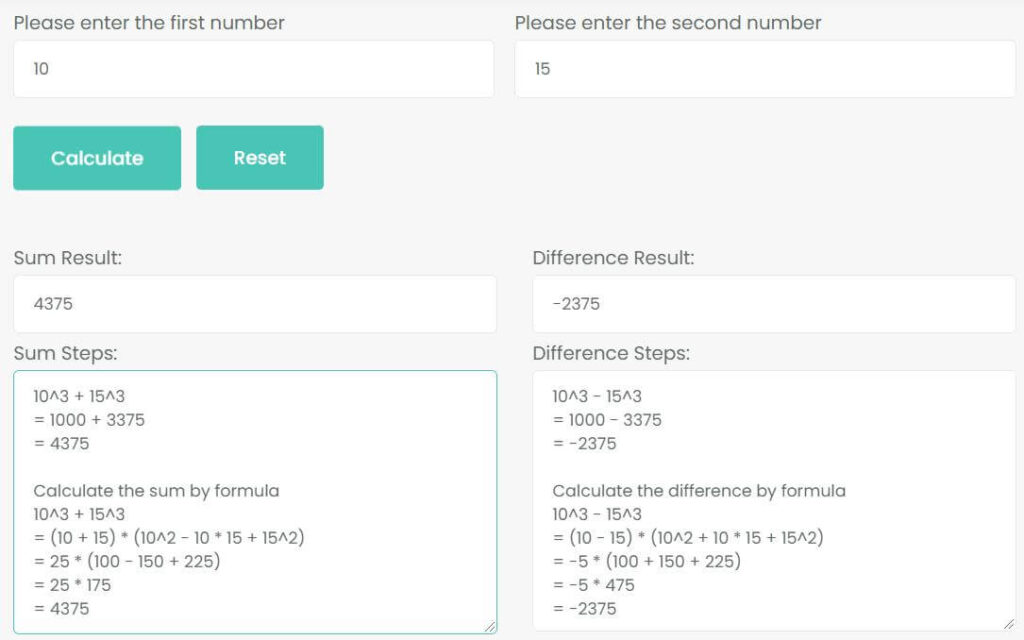As the picture shows, the sum of the cubes 10 and 15 is 4375, the difference of two cubes 10 and 15 is -2375.

Calculate using formula, find the sum of the cubes 16 and 12

16³ + 12³
= (16 + 12) * (16² – 16 * 12 + 12²)
= 28 * (256 – 192 + 144)
= 28 * 208
= 5824

The difference of two cubes 16 and 12 is

16³ – 12³
= (16 – 12) * (16² + 16 * 12 + 12²)
= 4 * (256 + 192 + 144)
= 4 * 592
= 2368

Use the sum and difference of two cubes calculator to calculate the sum and difference of the cubes 16 and 12.

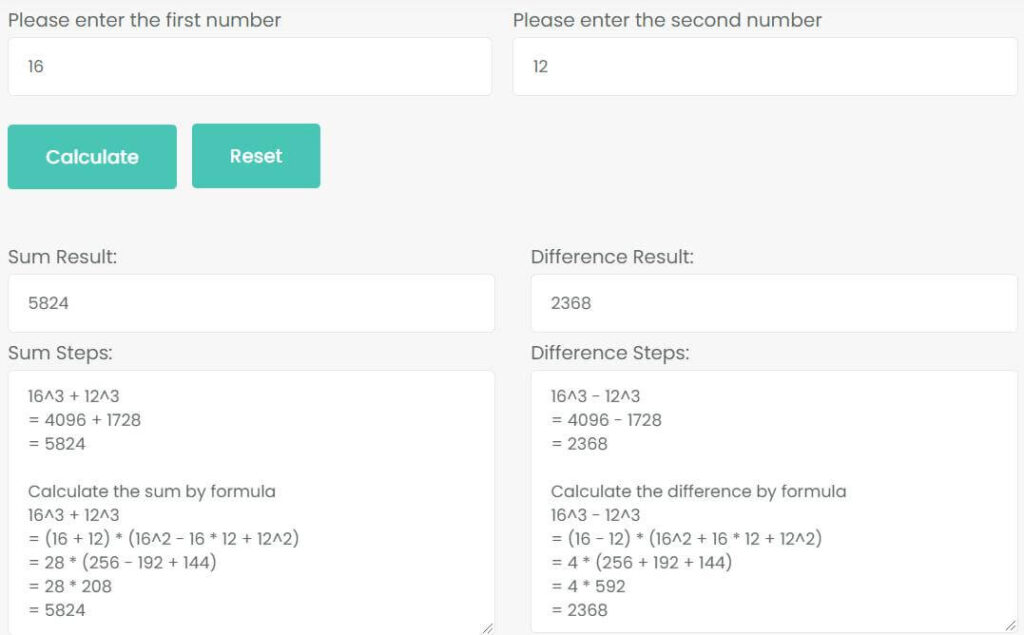As the picture shows, the sum of the cubes 16 and 12 is 5824, the difference of two cubes 16 and 12 is 2368.

Okay, make a try now.

Sum of Cubes Calculator

Sum of Consecutive Cubes Calculator

Sum of Cubes of First N Numbers Calculator