Sum and Nth Term of Harmonic Sequence Calculator

Sum and Nth Term of Harmonic Sequence Calculator is a free online tool for calculating the sum of harmonic sequence and the Nth term of a harmonic sequence.

A harmonic sequence (also called a harmonic progression) is a sequence in which the difference between two adjacent reciprocals is equal. The inverse of this difference is called the common harmonic difference. In other words, the reciprocal of an arithmetic sequence is a harmonic sequence, and the reciprocal of the common difference (tolerance) is the common harmonic difference.

For example, a harmonic sequence 12, 14, 16, 18. The difference between two adjacent reciprocals is 2. So, the common harmonic difference is 12.

Note that a harmonic sequence is not the same as a harmonic series. A harmonic series is just a special case of a harmonic sequence.

The formula for the sum of the harmonic sequence is

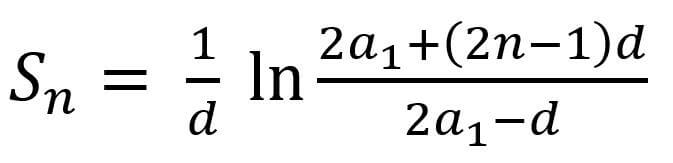Among them, d represents the common difference, the difference between two adjacent reciprocals. a₁ is the first item of the arithmetic sequence, which is the reciprocal of the first item of the harmonic sequence. n represents the number of items. ln represents the logarithm to base e.

For example, calculate the sum of the harmonic sequences 12, 14, 16, 18.

Substitute a₁ = 2, d = 2, n = 4 into the formula

S_n = 12 * ln 2 * 2 + (2 * 4 – 1) * 22 * 2 – 2

= 12 * ln 182

= 12 * ln9

= 1.0986

Because the harmonic sequence is the reciprocal form of the arithmetic sequence. Therefore, according to the formula of the Nth term of the arithmetic sequence, the formula for the Nth term of the harmonic sequence is

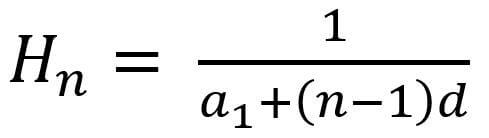Where a₁ represents the reciprocal of the first item of the harmonic sequence. d represents the common difference, the difference between two adjacent reciprocals. n represents the number of items.

For example, the 5th term of the harmonic sequence 12, 14, 16, 18.

Put a₁ = 2, d = 2 and n = 5 into the formula.

H_n = 12 + (5 – 1) * 2 = 110

Using the calculator is simple, follow these 4 steps:

Note that the inputs are the reciprocals of the harmonic sequence.

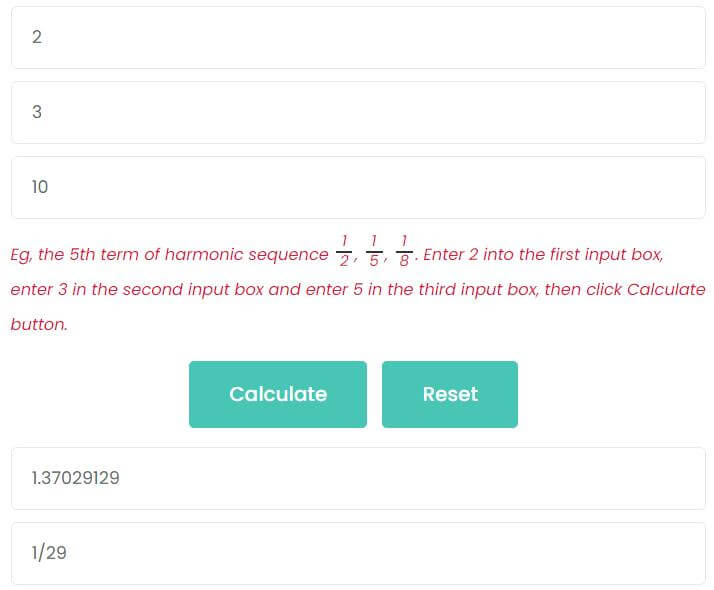
For example, calculate the sum and the 10th term of a harmonic sequence 12, 15, 18……

Enter 2 in the first input box.

Enter 3 in the second input box.

Enter 10 in the third input box.

As shown in the figure, the sum of the harmonic sequence is 1.37029129. The 10th term of the harmonic sequence is 129.