Square Sides Calculator

Find Side Length from Diagonal, Perimeter, or Area

If you’ve ever needed to calculate the side length of a square but weren’t sure where to start, you’re in the right place. Whether you’re working on a geometry problem, planning a construction project, or just satisfying your curiosity, the Square Sides Calculator is here to help. In this article, we will delve into the world of square side lengths, exploring three different methods to calculate them. Whether you have the diagonal, perimeter, or area of a square, we’ve got you covered.

Square Sides Calculator

Calculate Reset

What is Square Side Length

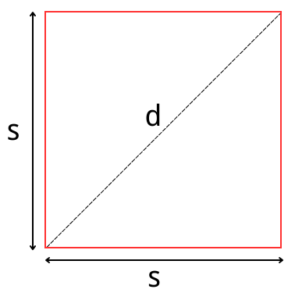
A square is a four-sided polygon with all sides of equal length and all angles of 90 degrees. This means that if you know one side length of a square, you automatically know the length of all four sides. But what if you’re given other properties of the square, like its diagonal, perimeter, or area? That’s where the Square Sides Calculator comes in handy.

How to Calculate Square Side Lengths

In this section, we’ll delve into the three methods for calculating square side lengths in detail. For each method, we’ll provide a clear formula and a step-by-step example.

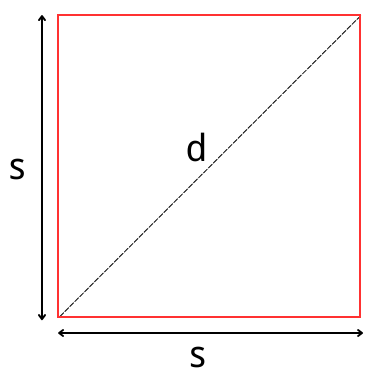
Method 1: Using the Diagonal

To calculate the side length (s) of a square when you know its diagonal (d), you can use the formula:

s = d / √2

Example:

Let’s say you have a square with a diagonal of 10 meters, and you want to find the length of its sides. Using the formula:

s = d / √2 = 10 / √2 = 7.07

So, the side length of the square is approximately 7.07 meters.

Method 2: Using the Square Perimeter

If you have the perimeter (P) of a square and want to find its side length (s), use the formula:

s = P4

Example:

Suppose you have a square with a perimeter of 20 centimeter. To find the side length:

s = P4 = 204 = 5

The side length of the square is 5 centimeter.

Method 3: Using the Square Area

When you know the area (A) of a square and need to determine its side length (s), use the formula:

s = √A

Example:

Imagine you have a square with an area of 49 square units. To calculate the side length:

s = √A = √49 = 7

The side length of the square is 7 units.

Square Sides Calculator Introduction

The Square Sides Calculator is a user-friendly tool designed for quick and accurate side length calculations. It’s especially useful when you have information about the diagonal, perimeter, or area of a square but need to find the side length for your calculations.

How to Use the Calculator

Using the Square Sides Calculator is straightforward:

1Select the method you want to use (Diagonal, Perimeter, or Area).
2Enter the known value into the appropriate field.
3Click the ``Calculate`` button. The calculated side length will be displayed.
4Click the Reset button to start a new calculation.

FAQs

Q: What is a square's side length?
A: The side length of a square is the measure of one of its four equal sides.

Q: What if I don't have any additional information about the square except its side length, can I find anything else?
A: Knowing the side length alone, you can calculate the square’s perimeter and area. Perimeter is 4s, and area is s².

Q: Are all four sides of a square always equal?
A: Yes, by definition, all sides of a square are equal in length.

Q: Can I calculate the side length of a square if I know its radius?
A: No, because a square does not have a traditional radius like a circle does.

Q: Is there a practical application for finding square side lengths?
A: Yes, it’s used in various fields like construction, engineering, and design to create and measure square objects.

Q: Can I use these methods for any square?
A: Yes, these methods apply to all squares, regardless of their size.

Q: Is there a quicker way to calculate square sides?
A: The Square Sides Calculator simplifies the process and provides instant results.

Q: What is the formula for finding a square's diagonal?
A: The formula is Diagonal = Side length * √2.

Q: Can I use these methods for rectangles or other shapes?
A: These methods are specific to squares but may differ for other shapes.

Q: Is there a limit to how many decimal places I should round to?
A: Typically, two decimal places are sufficient for most applications. The Square Sides Calculator retains 6 decimal places by default!

Q: Can I use this calculator on my mobile device?
A: Yes, the Square Sides Calculator is accessible from any device with an internet connection.

Conclusion

Calculating the side length of a square is an essential skill in geometry and various real-world scenarios. With the Square Sides Calculator and the methods outlined here, you can confidently find the side length using the square’s diagonal, perimeter, or area. Whether you’re solving math problems or working on construction projects, knowing how to find square sides is a valuable tool at your disposal.