Square Diagonal Calculator

Find Diagonal from Side Length, Perimeter, or Area

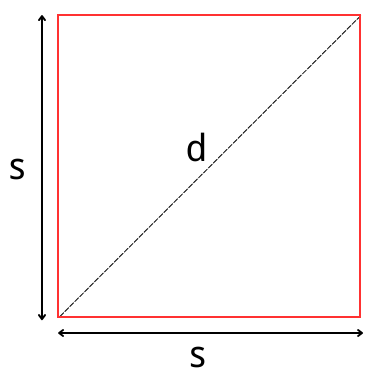
Are you looking to calculate the diagonal of a square? Whether you’re a student tackling geometry problems or someone in need of quick square diagonal measurements, our Square Diagonal Calculator is here to help. In this article, we’ll explore what a square diagonal is and provide you with step-by-step instructions on how to find it using three different methods: using the side length, square perimeter, or square area. Let’s dive in!

Square Diagonal Calculator

Calculate Reset

What is Square Diagonal

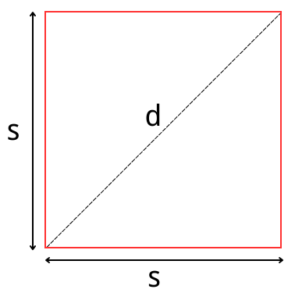
Before we delve into the calculations, let’s understand what a square diagonal is. In a square, the diagonal is the line segment that connects two opposite corners or vertices. As shown in the figure above, the dotted line segment is the diagonal line, usually represented by the letter d. It divides the square into two congruent right triangles, and it’s often used in various geometric and mathematical applications.

How to Calculate the Square Diagonal

In this section, we’ll explore three methods for calculating the diagonal of a square: using the side length, square perimeter, or square area. For each method, we’ll provide the formula and a step-by-step example.

Method 1: Using Side Length

This method uses the Pythagorean Theorem, where the diagonal is the hypotenuse of a right triangle formed by two sides of the square. The formula multiplies the side length by the square root of 2 to find the diagonal.

Diagonal (d) = Side Length (s) * √2

Example:

Let’s say you have a square with a side length of 10 units.

To find the diagonal, use the formula:

Diagonal (d) = Side Length (s) * √2 = 10 * √2 = 14.14

So, the diagonal is 14.14 units.

Method 2: Using Square Perimeter

This method utilizes the square’s perimeter, which is the sum of all four sides. By dividing the perimeter by 2√2, you can find the diagonal. The Formula:

Diagonal (d) = Perimeter (P) / (2√2)

Example:

Imagine you know the square’s perimeter is 40 units.

To calculate the diagonal, use the formula:

Diagonal (d) = Perimeter (P) / (2√2) = 40 / (2√2) = 14.14

Therefore, the diagonal of this square is 14.14 units.

Method 3: Using Square Area

This method is based on the relationship between the square’s area and its diagonal. By multiplying the area by 2 and taking the square root of the result, you can find the diagonal length. Below is the formula

Diagonal (d) = √(2 * A)

Example:

Suppose you have the area of the square, which is 50 square units.

To determine the diagonal, apply the formula:

Diagonal (d) = √(2 * A) = √(2 * 50) = 10

So, the diagonal of the square is 10 units.

Square Diagonal Calculator Introduction

Our Square Diagonal Calculator is designed to make your life easier when dealing with square-related calculations. Whether you’re working on school assignments, crafting projects, or architectural plans, knowing the diagonal length can be incredibly helpful.

How to Use the Calculator

Using our Square Diagonal Calculator is a breeze. Here’s a step-by-step guide:

1Select the method: Side, Perimeter, or Area.
2Input the known value: Whether you have the side length, square perimeter, or square area, enter it into the corresponding field.
3Click ``Calculate``: Hit the calculate button, and voila! The calculator will instantly display the diagonal of your square.
4Click the Reset button to start a new calculation.

FAQs

Q: What is the diagonal of a square?
A: The diagonal of a square is a line segment that connects two opposite corners or vertices of the square.

Q: Why is the diagonal of a square important?
A: The diagonal is used in various mathematical and geometric calculations. It’s also handy for measuring distances in crafting and construction projects.

Q: How can I calculate the square diagonal without a calculator?
A: You can use the Pythagorean Theorem: Diagonal length (d) = Side length (s) * √2.

Q: What are some real-world applications of square diagonals?
A: Square diagonals are used in architecture for measuring room dimensions, in art for creating precise geometric designs, and in woodworking for making accurate cuts.

Q: Is the square diagonal always longer than the sides?
A: Yes, the diagonal is always longer than the sides in a square. The relationship between the diagonal and side length is d = s * √2.

Q: Can I use the square diagonal to find its area or perimeter?
A: Yes, you can. Knowing the diagonal, you can easily calculate the square’s area and perimeter using the diagonal length formula.

Q: What if I have the perimeter of the square? How can I find the diagonal?
A: You can use our calculator. Input the perimeter, and it will give you the diagonal length.

Q: Are the two diagonals of a square equal in length?
A: Yes, in a square, both diagonals are equal in length and bisect each other.

Q: Is the square diagonal calculator accurate?
A: Yes, our calculator provides accurate results for finding the diagonal length of a square.

Conclusion

Calculating the diagonal of a square doesn’t need to be a complex task. With our Square Diagonal Calculator, you can find this essential measurement swiftly and accurately, whether you have the side length, square perimeter, or square area. Embrace the convenience of this tool for your mathematical, artistic, or practical needs.