Square Calculator
Input any one parameter of a square (side length, perimeter, area, or diagonal) and get the remaining three values instantly.
Find Side Length, Perimeter, Area, or Diagonal of Square
Side
Perimeter
Area
Diagonal
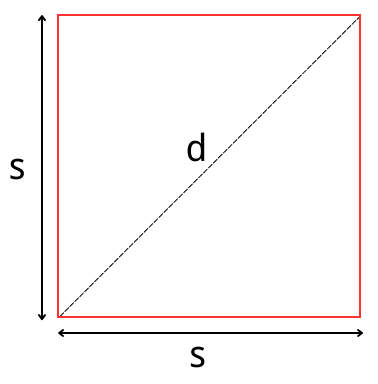
Properties of a Square
A square has equal side lengths, and all its angles are right angles. The relationships between its properties are as follows:
Perimeter and Side Length Relation: \( \text{Perimeter} = 4 \times \text{Side Length} \)
Area and Side Length Relation: \( \text{Area} = \text{Side Length}^2 \)
Diagonal and Side Length Relation: \( \text{Diagonal} = \text{Side Length} \times \sqrt{2} \)
These formulas are the foundation for calculating all properties of a square.
How to Calculate Square Properties
If Side Length (\( a \)) is Known
- Perimeter: \( C = 4a \)
- Area: \( A = a^2 \)
- Diagonal: \( d = a \sqrt{2} \)
If Perimeter (\( C \)) is Known
- Side Length: \( a = \frac{C}{4} \)
- Area: \( A = \left(\frac{C}{4}\right)^2 \)
- Diagonal: \( d = \frac{C}{4} \times \sqrt{2} \)
If Area (\( A \)) is Known
- Side Length: \( a = \sqrt{A} \)
- Perimeter: \( C = 4 \times \sqrt{A} \)
- Diagonal: \( d = \sqrt{A} \times \sqrt{2} \)
If Diagonal (\( d \)) is Known
- Side Length: \( a = \frac{d}{\sqrt{2}} \)
- Perimeter: \( C = \frac{d}{\sqrt{2}} \times 4 \)
- Area: \( A = \left(\frac{d}{\sqrt{2}}\right)^2 \)
Examples
Example 1: Given the side length \( a = 6 \) of the square, find the perimeter, area, and diagonal.
Solution:
Perimeter:
\( C = 4 \times 6 = 24 \)
Area:
\( A = 6^2 = 36 \)
Diagonal:
\( d = 6 \times \sqrt{2} \approx 8.49 \)
Result: The perimeter is \( 24 \), the area is \( 36 \), and the diagonal is approximately \( 8.49 \).
Example 2: Given the perimeter \( C = 20 \) of a square, find the side length, area, and diagonal.
Solution:
Side Length:
\( a = \frac{20}{4} = 5 \)
Area:
\( A = 5^2 = 25 \)
Diagonal:
\( d = 5 \times \sqrt{2} \approx 7.07 \)
Result: The side length is \( 5 \), the area is \( 25 \), and the diagonal is approximately \( 7.07 \).
Example 3: Given the area \( A = 144 \) of a square, find the side length, perimeter, and diagonal.
Solution:
Side Length:
\( a = \sqrt{144} = 12 \)
Perimeter:
\( C = 4 \times 12 = 48 \)
Diagonal:
\( d = 12 \times \sqrt{2} \approx 16.97 \)
Result: The side length is \( 12 \), the perimeter is \( 48 \), and the diagonal is approximately \( 16.97 \).