Sector Calculator
Input the radius and central angle of a sector (in degrees or radians) to instantly calculate its arc length, chord length, and area.
Calculate Arc Length, Chord Length and Sector Area
Arc Length
Chord Length
Sector Area
What Is a Sector?
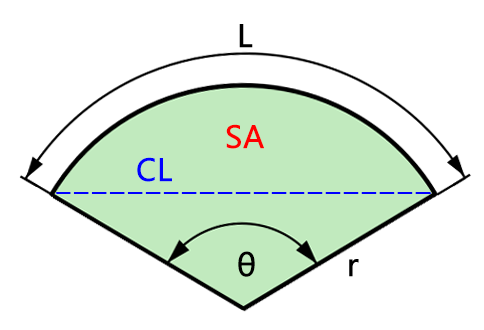
A sector is a portion of a circle defined by a central angle, comprising the arc and two radii connecting the arc's endpoints to the center. Using the radius \( r \) and central angle \( \theta \) (in degrees or radians), various properties of the sector can be calculated.
How to Calculate Sector Parameters
Arc Length
The arc length is the curved boundary of the sector.
- For degrees: \( L = 2 \pi r \times \frac{\theta}{360} \)
- For radians: \( L = r \times \theta \)
Chord Length
The chord length is the straight line connecting the endpoints of the arc. \( c = 2r \times \sin\left(\frac{\theta}{2}\right) \) If \( \theta \) is in degrees, convert it to radians using \( \theta \times \frac{\pi}{180} \).
Area
The area of the sector represents its surface area.
- For degrees: \( A = \pi r^2 \times \frac{\theta}{360} \)
- For radians: \( A = \frac{1}{2} r^2 \theta \)
For example: Given Radius \( r = 10 \), Central angle \( \theta = 60^\circ \), find the Arc length \( L \), Chord length \( c \), and Area \( A \).
Solution:
Arc Length:
\( L = 2 \pi \times 10 \times \frac{60}{360} \approx 10.47 \)
Chord Length:
\( c = 2 \times 10 \times \sin\left(\frac{60 \times \pi}{180} / 2\right) \approx 10 \)
Area:
\( A = \pi \times 10^2 \times \frac{60}{360} \approx 52.36 \)
Result: Arc length \( L \approx 10.47 \), Chord length \( c \approx 10 \), Area \( A \approx 52.36 \).