Right Triangle Calculator

Calculate Sides, Angles, Perimeter, and Area

Welcome to the Right Triangle Calculator. In this article, we’ll learn how to calculate sides, angles, perimeter, and area with ease.

Right Triangle Calculator

Calculate Reset

What is a Right Triangle

First things first, what exactly is a right triangle? A right triangle is a triangle that features one right angle, which measures precisely 90 degrees. This right angle divides the triangle into two smaller triangles, each with its own unique set of properties.

How to Calculate the Sides, Angles, Perimeter, and Area of a Right Triangle

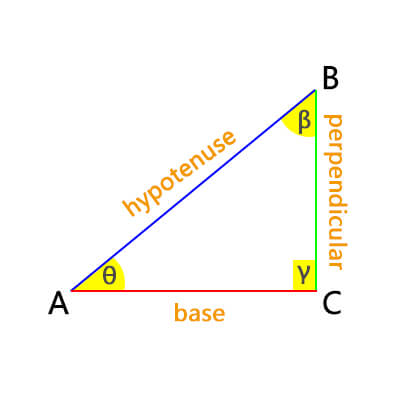Calculating the sides, angles, perimeter, and area of a right triangle is a multifaceted task. Here’s a step-by-step guide that will equip you with the necessary skills:

Given Two Sides:

Identify the Known Sides: Determine which sides of the right triangle are known to you. These will be labeled as the base (B), perpendicular (P), and hypotenuse (H) sides.

Calculate the Unknown Side: If you know the lengths of two sides (for example, B and P), you can use the Pythagorean Theorem to find the length of the third side (H). The Pythagorean Theorem states:

H² = B² + P²

Find Angles: Once you have the sides, you can find the angles using trigonometric functions. For example, to find Angle θ, you can use the tangent function:

tan(θ) = PB

Given One Angle and One Side:

Identify the Known Angle and Side: Determine which angle (θ) and side (S) are known to you.

Calculate Other Angles: You can find the remaining angle (90° – θ) using the fact that the sum of angles in a triangle is always 180 degrees.

Determine Unknown Side: To calculate the unknown side (U), use trigonometric functions. For example, to find the hypotenuse, you can use the sine function:

H = Ssin(θ)

Calculating Perimeter:

The perimeter of a right triangle is the sum of the lengths of its three sides. Simply add the lengths of the base, perpendicular, and hypotenuse.

Perimeter = B + H + P

Calculating Area:

The area of a right triangle can be calculated using the formula:

Area = B * P2.

Multiply the lengths of the base and perpendicular, and then divide by 2.

FAQs

Q: What is a right triangle, and what makes it unique?
A: A right triangle is a triangle with one right angle (90 degrees). This characteristic sets it apart from other types of triangles.

Q: What is the Pythagorean Theorem, and how is it used in right triangles?
A: The Pythagorean Theorem states that in a right triangle, the square of the hypotenuse’s length is equal to the sum of the squares of the other two sides. It’s used to find missing sides in right triangles.

Q: How can I find the angles in a right triangle?
A: You can use trigonometric functions like sine, cosine, and tangent to find the angles based on the known sides.

Q: What is the perimeter of a right triangle, and how is it calculated?
A: The perimeter is the sum of the lengths of the three sides. To calculate it, add the lengths of the base, perpendicular, and hypotenuse.

Q: What is the area of a right triangle, and how is it calculated?
A: The area is half of the product of the base and perpendicular. You can use the formula: Area= 1/2 ×B×P.

Q: Can a right triangle have two right angles?
A: No, a right triangle, by definition, has exactly one right angle.

Q: What is the relationship between the angles in a right triangle?
A: In a right triangle, one angle is always 90 degrees, and the other two angles add up to 90 degrees.

Q: How do I determine which side is the base, perpendicular, and hypotenuse?
A: The side opposite the right angle is the hypotenuse. The side adjacent to the right angle is typically called the base, and the remaining side is the perpendicular.

Q: Is it possible to have negative side lengths in a right triangle?
A: No, side lengths in geometry are always considered positive.

Q: What real-world applications involve right triangle calculations?
A: Right triangles are commonly used in fields like construction, engineering, architecture, and navigation for measuring heights, distances, and angles.

Conclusion

With this newfound knowledge of the right triangle calculator, you’ve acquired the skills to calculate sides, angles, perimeter, and area with confidence. Whether you’re tackling mathematical problems or practical applications in construction and design, the right triangle calculator is your trusted companion.