Rhombus Diagonals Calculator

3 Ways to Calculate Rhombus Diagonal Lengths

Explore the Rhombus Diagonals Calculator, a user-friendly tool for precise geometry calculations. Calculate rhombus diagonal lengths effortlessly based on side, angle, perimeter, and area inputs.

Rhombus Diagonals Calculator

Calculate Reset

What is a Rhombus Diagonal

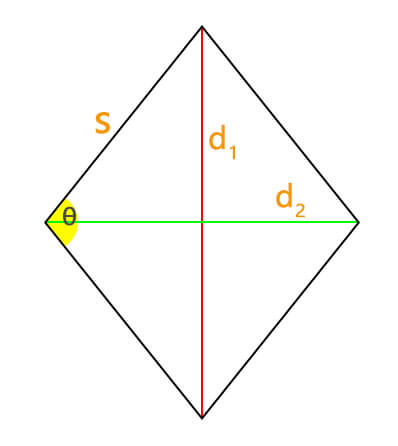A rhombus, often referred to as a diamond, is a quadrilateral with all sides of equal length. Diagonals of a rhombus are the line segments connecting opposite vertices (d₁ and d₂ in the picture), forming a crucial aspect of its geometry. The Rhombus Diagonals Calculator streamlines the process of determining these diagonal lengths based on various inputs.

How to Calculate the Diagonal Length of a Rhombus

Calculating the length of the diagonals involves several methods. Let’s explore three of them with step-by-step instructions:

Side Method

Identify the side length (s) and angle (θ) formed by one side and its adjacent side.

Use the formula

d1 = s * √(2+2cos(θ))

d2 = s * √(2 – 2cos(θ))

Example: If the side length is 8 units, and the angle formed is 60 degrees, the diagonal lengthsare

d1 = s * √(2 + 2cos(θ)) = 8 * √(2 + 2cos(60°)) = 13.856 units

d2 = s * √(2 – 2cos(θ)) = 8 * √(2 – 2cos(60°)) = 8 units

Perimeter Method

Identify the perimeter (P) and angle (θ) formed by one side and its adjacent side.

Use the formula

d1 = P/4 * √(2 + 2cos(θ))

d2 = P/4 * √(2 – 2cos(θ))

Example: If the perimeter is 24 units, and the angle formed is 45 degrees, the diagonal lengthsare

d1 = P/4 * √(2 + 2cos(θ)) = 24/4 * √(2 + 2cos(45°)) = 11.087 units

d2 = P/4 * √(2 – 2cos(θ)) = 24/4 * √(2 – 2cos(45°)) = 4.592 units

Area Method

Identify the area (A) and angle (θ) formed by one side and its adjacent side.

Use the formula

d1 = √((2A + 2A * cos(θ)) / sin(θ))

d2 = √((2A – 2A * cos(θ)) / sin(θ))

Example: If the area is 48 square units, and the angle formed is 30 degrees, the diagonal lengthsare

d1 = √((2A + 2A * cos(θ)) / sin(θ)) = √((2 * 48 + 2 * 48 * cos(30°)) / sin(30°)) = 18.928 units

d2 = √((2A – 2A * cos(θ)) / sin(θ)) = √((2 * 48 – 2 * 48 * cos(30°)) / sin(30°)) = 5.072 units

FAQs

Q: Can the calculator handle decimal values in angle measurements?
A: Yes, the calculator accommodates both whole numbers and decimal values for angle measurements.

Q: Is there a specific unit requirement for side lengths?
A: The calculator is unit-agnostic, allowing for the input of side lengths in any consistent unit of measurement.

Q: How is rounding managed in the final diagonal length output?
A: The calculator typically provides diagonal length results rounded to 6 decimal places.

Q: What makes the diagonals of a rhombus unique compared to other quadrilaterals?
A: The diagonals of a rhombus bisect each other at right angles, setting them apart as perpendicular bisectors.

Q: Do the diagonals of a rhombus have equal lengths?
A: Not necessarily equal, but bisected vertically.

Q: How are the diagonals related to the sides and angles of a rhombus?
A: The diagonals of a rhombus divide it into four congruent right-angled triangles, establishing a clear relationship with the sides and angles.

Q: Can the diagonals of a rhombus be used to determine its area?
A: Yes, the diagonals of a rhombus play a crucial role in calculating its area using the formula (Diagonal1 * Diagonal2) / 2.

Q: Are the diagonals of a rhombus always perpendicular?
A: Yes, the diagonals of a rhombus are always perpendicular to each other, forming right angles at their point of intersection.

Q: How do the diagonals bisect the angles of a rhombus?
A: Each diagonal of a rhombus bisects the opposite angle, creating two congruent smaller angles.

Q: Are the diagonals of a rhombus symmetry axes?
A: Yes, the diagonals of a rhombus serve as symmetry axes, dividing the rhombus into two mirror-image halves.

Q: How do the diagonals of a rhombus relate to its center?
A: The point where the diagonals of a rhombus intersect is the center of the rhombus, and each diagonal is a radius of the circumscribed circle.

Q: Can the diagonals of a rhombus be used to find its perimeter?
A: While the diagonals alone do not directly determine the perimeter, understanding their length and relationship to sides aids in comprehensive perimeter calculations.