Regular Polygon Side Length Calculator - 5 Methods Explained

Welcome to the world of polygons! Ever wondered how to find the length of a side when you know the perimeter, area, apothem, or the radius of the inscribed or circumscribed circle? Fret not, as the Regular Polygon Side Length Calculator is here to unravel the mystery and provide you with the answers you seek.

Regular Polygon Side Length Calculator

Calculate Reset

Definition

Before diving into the calculations, let’s define a regular polygon. A regular polygon is a polygon with equal sides and equal angles. Each side and angle is identical, creating a harmonious and balanced shape.

How to Calculate the Side Length of a Regular Polygon

Now, let’s explore the methods to find the side length based on different parameters.

Perimeter Method

The formula to calculate the side length (s) of a regular polygon when the perimeter (P) is known is:

s = P/n

Where n is the number of sides in the polygon.

Example: Suppose we have a regular hexagon with a perimeter of 30 units. Using the formula:

s = P/n = 30/6 = 5 units

Therefore, each side of the hexagon is 5 units long.

Area Method

To find the side length (s) when the area (A) and the number of sides (n) are given, the formula is:

s= √(4A * tan(π/n)/n)

Example:For a regular pentagon with an area of 50 square units, the side length is

s = √(4A* tan(π/n)/n) = √(4 * 50* tan(π/5)/5) = 5.39units

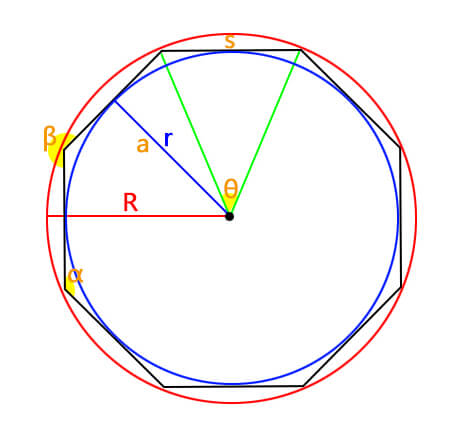
Apothem Method

If the apothem (a) and the number of sides (n)are known, the formula becomes:

s = 2a * tan(π/n)

Example: Let’s take a regular hexagon with an apothem (a) of 8 units. Using the formula:

s = 2a * tan(π/n) = 2 * 8 * tan(π/6) =9.238 units

So, the side length of this regular hexagon is 9.238 units.

Inscribed Circle Radius Method

When the radius of the inscribed circle (r) and the number of sides (n) are given, the formula is:

s = 2r * tan(π/n)

Example: Imagine a regular heptagon with a radius of the inscribed circle (r) equal to 6 units. So, the side length of the regular heptagon is:

s = 2r * tan(π/n) = 2 * 6 * tan(π/7) = 5.779units

Circumscribed Circle Radius Method

If you have the radius of the circumscribed circle (R) andthe number of sides (n), the formula is:

s = 2R * sin(π/n)

Example: Let’s explore a regular nonagon with a circumscribed circle radius (R) of 10 units. Using the formula:

s = 2R * sin(π/n) = 2 * 10 * sin(π/9) = 6.84 units

Calculate to unveil the side length. The side length is 6.84 units.

FAQs

Q: Can a regular polygon have an odd number of sides?
A: Yes, a regular polygon can have an odd or even number of sides. For example, a triangle (3 sides) is a regular polygon.

Q: What is the minimum number of sides for a regular polygon?
A: A regular polygon must have at least three sides.

Q: Can a regular polygon have sides of different lengths?
A: No, in a regular polygon, all sides must be of equal length.

Q: Is the apothem always smaller than the radius of the inscribed circle?
A: Yes, the apothem is always smaller than the radius of the inscribed circle.

Q: What is the maximum number of sides for a regular polygon?
A: Theoretically, a regular polygon can have an infinite number of sides.

Q: Is the formula for side length the same for all regular polygons?
A: Yes, the formula is general and applies to all regular polygons.

Q: Can a regular polygon be concave?
A: No, a regular polygon is always convex.

Q: Does the shape of a regular polygon change if the side length is altered?
A: Yes, changing the side length will alter the overall shape of the regular polygon.

Q: What is the difference between the inscribed and circumscribed circles?
A: The inscribed circle is tangent to all sides of the polygon, while the circumscribed circle passes through all vertices.

Q: Is the apothem always perpendicular to a side of the polygon?
A: Yes, the apothem is always perpendicular to a side.

Q: Can a regular polygon have sides of zero length?
A: No, the sides must have a positive length.

Q: Are there regular polygons in nature?
A: Yes, various natural formations exhibit shapes that approximate regular polygons.

Q: Can a regular polygon have curved sides?
A: No, a regular polygon consists of straight sides.

Conclusion

Understanding regular polygons and their side lengths adds a layer of appreciation for their geometric elegance. The Regular Polygon Side Length Calculator simplifies these calculations, whether you’re dealing with triangles, hexagons, or polygons with an extensive number of sides, this calculator can quickly figure out their side lengths.