Regular Polygon Calculator

Calculate the perimeter, area, internal and external angles, central angles, number of diagonals, and radii of inscribed and circumscribed circles of a regular polygon.

Welcome to the Regular Polygon Calculator—a versatile tool designed to unravel the secrets of these geometric wonders. This calculator goes beyond the basics, allowing you to effortlessly compute various parameters of a regular polygon, from perimeter, area, angles to the radii of inscribed and circumscribed circles, and even more.

Regular Polygon Calculator

Calculate Reset

Definition

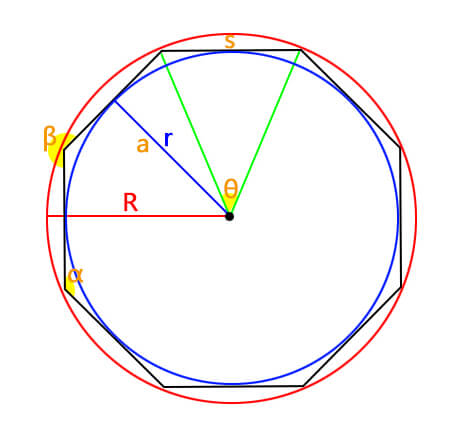A regular polygon is a closed figure with equal sides and equal angles. Understanding its properties involves delving into key parameters, including perimeter, area, internal and external angles, central angle, number of diagonals, apothem, and radii of inscribed and circumscribed circles.

Perimeter: The sum of all sides.

Area: The space enclosed by the polygon.

Internal Angle: The measure of an angle inside the polygon (α in the picture).

Outer Angle: The supplementary angle to the internal angle (β in the picture).

Central Angle: The angle formed at the center of the polygon (θ).

Diagonals Number: The count of straight lines connecting non-adjacent vertices.

Apothem: The distance from the center to the midpoint of a side (h).

Inscribed Circle Radius: The radius of the circle inscribed within the polygon (r, same as Apothem).

Circumscribed Circle Radius: The radius of the circle passing through all vertices (R).

How to Calculate Various Parameters of a Regular Polygon

Let’s delve into the step-by-step calculations for different parameters of a regular polygon using the Regular Polygon Calculator.

1. Perimeter and Area Calculation

Perimeter (P): The perimeter of a regular polygon is calculated by multiplying the number of sides (n) by the length of each side (s).

P = n * s

Area (A): Area is calculated by side length (s) and number of sides (n), using the following formula:

A = 1/4 * n * s² * cot(π/n)

Also, the area is found by multiplying the perimeter by the apothem (a) and dividing the result by 2.

A = (P * a)/2

Example: Consider a regular hexagon with a side length (s) of 6 units.

The perimeter is

P= 6 * 6 =36 units

The area is

A = 1/4 * n * s² * cot(π/n) = 1/4 * 6 * 6² * cot(π/6) = 93.53 square units

2. Internal and External Angles

Internal Angle (α): The internal angle of a regular polygon is given by the formula

α = 180 * (n – 2)/n

External Angle (β): The external angle is complementary to the internal angle, i.e.,

β =180 – α

Example: For a regular pentagon, the internal angle is

α = 180 * (n – 2)/n = 180 * (5 – 2)/5 =108degrees

The external angle is

β =180 – α = 180 – 108 = 72 degrees

3. Central Angle Calculation

Central Angle (θ): The central angle is found by dividing 360 degrees by the number of sides (n).

θ = 360/n

Example: For an octagon, the central angle is

θ = 360/n = 360/8 = 45 degrees

4. Number of Diagonals Calculation

Number of Diagonals (D): The number of diagonals in a regular polygon is given by

D = n * (n – 3)/2

Example: A regular heptagon, the number of diagonals is

D = n * (n – 3)/2 = 7 * (7 – 3)/2 = 14

5. Apothem Calculation

Apothem (a): The apothem is calculated using the formula

a = s/(2 * tan(π/n))

where s is the side length.

Example: For a regular nonagonwith a side length (s) of 8 units, the apothemis

a = s/(2 * tan(π/n)) = 8/(2 * tan(π/9)) = 10.9899 units

6. Radii of Inscribed and Circumscribed Circles Calculation:

Radius of Inscribed Circle (r): The inscribed circle radiusis calculated using the formula

r = s/2 * cot(π/n) = s/(2 * tan(π/n))

Radius of Circumscribed Circle (R): The circumscribedcircle radius is calculated using the formula

R = s/2 * csc(π/n) = s/(2 * sin(π/n))

where s is the side length, n is the number of sides.

Example: For a regular decagon with a side length (s) of 5 units, the inscribed circle radius is

r = s/(2 * tan(π/n)) = 5/(2 * tan(π/10)) = 7.6942 units

The circumscribed circle radius is

R = s/(2 * sin(π/n)) = 5/(2 * sin(π/10)) = 8.09 units

FAQs:

Q: How is the apothem determined for area calculations?
A: The apothem is a perpendicular distance from the center to a side. It can be calculated using trigonometry.

Q: Is the calculator suitable for polygons with a large number of sides?
A: Yes, the calculator accommodates various polygon sizes, ensuring accuracy.

Q: Can I use this calculator for 3D regular polygons?
A: No, the calculator is designed for two-dimensional regular polygons.

Q: Are the results rounded off, and how many decimal places are provided?
A: Yes, up to 6 decimal places.

Q: Can I input fractional values for side length?
A: Absolutely! The calculator accommodates both whole numbers and fractional values for precise calculations.

Q: Is the apothem the same as the radius of the inscribed circle?
A: Yes, in a regular polygon, the apothem is equivalent to the radius of the inscribed circle.

Q: What is the significance of the circumscribed circle in a regular polygon?
A: The circumscribed circle is the circle that passes through all the vertices of the regular polygon, and its radius holds geometric significance.

Q: How does the calculator determine the number of diagonals?
A: The formula for calculating diagonals in a regular polygon is employed, providing an accurate count.

Q: Does the calculator store or track user data?
A: No, the calculator is developed with user privacy in mind and does not store or track any user data.

Conclusion

As you journey into the realm of regular polygons, let the Regular Polygon Calculator be your guiding star. This intuitive tool not only simplifies calculations but also enhances your understanding of symmetrical shapes. Whether it is basic calculations of perimeter, area, internal angles, or advanced calculations of radius of inner and outer circles, apothem, and number of diagonals, this calculator can easily solve it.