Rectangle Calculator
Input any two parameters (length, width, perimeter, area, or diagonal) and instantly calculates all the rectangle's properties.
Calculate Length, Width, Perimeter, Area & Diagonal
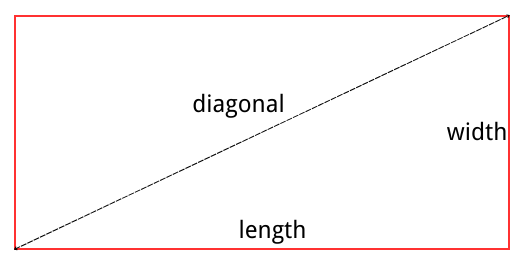
Length
Width
Perimeter
Area
Diagonal
Rectangle Calculator Overview
This tool calculates the following rectangle properties when given any two parameters:
- Sides (Length (\(l\)) or Width (\(w\)))
- Perimeter (\(P\))
- Area (\(A\))
- Diagonal (\(d\))
Key Rectangle Relationships
Rectangles follow these mathematical relationships between their properties:
Perimeter Formula: \( P = 2l + 2w \)
Area Formula: \( A = l \times w \)
Diagonal Formula: \( d = \sqrt{l^2 + w^2} \)
Using these equations, all rectangle properties can be determined if any two are known.
How to Calculate Rectangle Properties
1. Given Length (\(l\)) and Width (\(w\)):
- Perimeter: \( P = 2l + 2w \)
- Area: \( A = l \times w \)
- Diagonal: \( d = \sqrt{l^2 + w^2} \)
2. Given Length (\(l\)) and Perimeter (\(P\)):
- Width: \( w = \frac{P}{2} - l \)
- Calculate the other properties as above.
3. Given Length (\(l\)) and Area (\(A\)):
- Width: \( w = \frac{A}{l} \)
- Use the length and width to find \(P\) and \(d\).
Given Length (\(l\)) and Diagonal (\(d\)):
- Width: \( w = \sqrt{d^2 - l^2} \)
- Use the length and width to find \(P\) and \(A\).
5. Given Perimeter (\(P\)) and Area (\(A\)):
Use the formulas for \(P = 2l + 2w\) and \(A = l \times w\) (sum-product relation) to create a quadratic equation. Solve for \(l\) and \(w\).
6. Given Perimeter (\(P\)) and Diagonal (\(d\)):
- Combine \(P = 2l + 2w\) and \(d = \sqrt{l^2 + w^2}\) to solve for \(l\) and \(w\).
7. Given Area (\(A\)) and Diagonal (\(d\)):
- Use \(A = l \times w\) and \(d = \sqrt{l^2 + w^2}\) to solve for \(l\) and \(w\).
Examples
Example 1: Known Length (\(l = 8\)) and Width (\(w = 6\)), Find the Perimeter, Area and Diagonal
Solution:
Perimeter:
\( P = 2 \times 8 + 2 \times 6 = 28 \)
Area:
\( A = 8 \times 6 = 48 \)
Diagonal:
\( d = \sqrt{8^2 + 6^2} = \sqrt{64 + 36} = \sqrt{100} = 10 \)
Example 2: Known Perimeter (\(P = 28\)) and Area (\(A = 48\)), Find the Length, Width and Diagonal.
Solution:
Solve for Length and Width:
\( l = \frac{28}{2} - w = 14 - w \)
\( w = \frac{A}{l} = \frac{48}{l} \)
Solve the quadratic equation to find \(l = 8\) and \(w = 6\).
Diagonal:
\( d = \sqrt{8^2 + 6^2} = \sqrt{100} = 10 \)
Example 3: Known Perimeter (\(P = 28\)) and Diagonal (\(d = 10\)), Find the Length and Width.
Solution:
According to the perimeter formula, calculate the sum of length and width:
\( P = 2l + 2w \)
\( l + w = \frac{P}{2} = 14 \)
Based on the diagonal formula, calculate the product of length and width:
\( d = \sqrt{l^2 + w^2} \)
\( l^2 + w^2 = d^2 = 100 \)
\( (l + w)^2 = 14^2 \)
\( l^2 + w^2 + 2lw = 196 \)
\( 100 + 2lw = 196 \)
\( l \times w = 48 \)
Using the sum and product relation to construct the equation:
\(t^2 - 14t + 48 = 0 \)
Using the quadratic formula:
\( t = \frac{14 \pm \sqrt{14^2 - 4 \times 48}}{2} \)
\( l = 8, \, w = 6 \)
Result: The length is \( 8 \), the width is \( 6 \).
Example 4: Known Area (\(A = 48\)) and Diagonal (\(d = 10\)), Find the Length and Width.
Solution:
According to the area formula, calculate the product of length and width:
\( l \times w = 48 \)
Based on the diagonal formula, calculate the sum of length and width:
\( d = \sqrt{l^2 + w^2} \)
\( l^2 + w^2 = 100 \)
\( l^2 + w^2 + 2lw = 100 + 2 \times 48 \)
\( (l + w)^2 = 196 \)
\( l + w = \sqrt{196} \)
\( l + w = 14 \)
Using the same sum-product formula (the steps are the same as in Example 3), we can solve for the length and width to be 8 and 6.