The power mean calculator is a free online tool for calculating the power mean of a set of numbers.
What is power mean?
How to calculate the power mean?
- Find the p power of each number.
- Add up all the values of the p power.
- Calculate the mean of p-power values.
- Calculate the power The p-root of the mean.
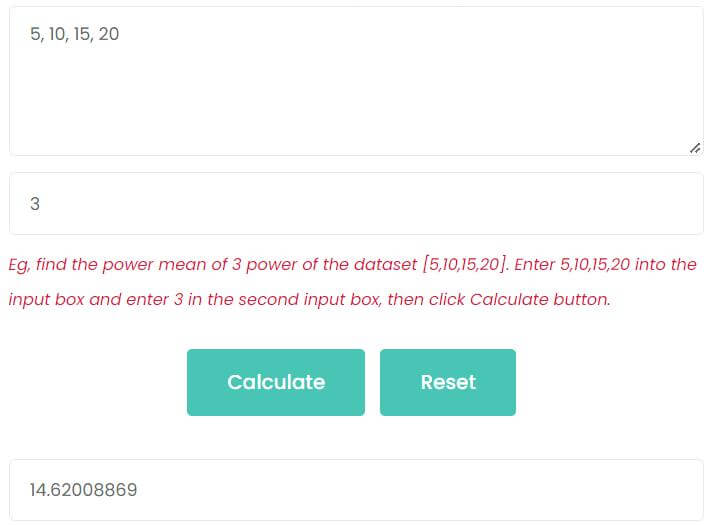
For example, find the power mean of 3 power of the dataset [5,10,15,20].
M3 = (53 + 103 + 153 + 2034)1/3
= (125 + 1000 + 3375 + 80004)1/3
= (125004)1/3
= (3125)1/3
= 14.62
How to use the power mean calculator
Using the calculator is simple, follow these 2 steps:
- Enter numbers in the first input box. Separate each number with a comma or newline.
- Enter the p power in the second input box, a non-zero real number.
- Click Calculate button to calculate the power square of input numbers, or click Reset button to start a new calculation.
Like the example above. Enter 5, 10, 15, 20 in the first input box and enter 3 in the second input box. Then, click Calculate button.
As shown in the figure, the result of the mean square calculator calculation is also 14.62.
Latest Calculators
Standard Form to Slope-Intercept Form Calculator
Slope Intercept Form Calculator
Slope Calculator: Calculate Slope, X-Intercept, Y-Intercept
Reciprocal of Complex Number Calculator
Conjugate Complex Number Calculator
Modulus of Complex Number Calculator
Profit Percentage Calculator: Calculate Your Profitability Easily
Attendance and Absence Percentage Calculator
Latest Checkers
Check if the given number is an almost perfect number.
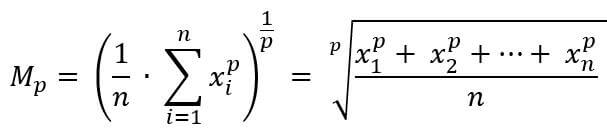 Where p and xi are both greater than 0. n is the total number of numbers in the dataset.
Where p and xi are both greater than 0. n is the total number of numbers in the dataset.