Perfect Square Trinomial Checker

Welcome to the Perfect Square Trinomial Checker, which can quickly help you check if a trinomial is a perfect square trinomial.

Perfect Square Trinomial Checker

ax² + bx + c

Eg, Is x² - 10x + 25 a perfect square trinomial? Enter 1 into the first input box, enter -10 into the second input box and enter 25 into the third input box. Then click Calculate button.

Calculate Reset

What is a perfect square trinomial?

A perfect square trinomial is an algebraic expression obtained from squaring a binomial expression. The binomial expression consists of a variable and a constant, and a trinomial expression consists of three terms.

In other words, if a trinomial expression can be factorised to get a square of a binomial expression, then the given trinomial expression is a perfect square trinomial.

The perfect square trinomial expression formula is:

(ax)² + 2abx + b² = (ax + b)²

(ax)² – 2abx + b² = (ax – b)²

When a trinomial expression is given as ax²+ bx + c, then the trinomial expression will be a perfect square trinomial if the condition b² = 4ac is met. This condition holds true even if b is negative because the condition checks for b² which results in a positive integer.

When a binomial a + b is given, you can calculate the perfect square trinomial by squaring the binomial as follows:

(a + b)² = a² + 2ab + b²

When the binomial is a - b, the perfect square trinomial is

(a – b)² = a² – 2ab + b²

How to check if a trinomial is a perfect square trinomial?

To determine whether a trinomial, ax²+ bx + c, is a perfect square trinomial you must factorize the trinomial expression and find the resulting binomials. When the answer is a square of a binomial, the given expression is a perfect square trinomial. Alternately, you can calculate whether the trinomial expression is a perfect square trinomial by checking whether the b² = 4ac condition is met.

For example, to find whether the trinomial x² + 14x + 49 is a perfect square trinomial, you can check for the condition b² = 4ac. Here, a = 1, b = 14 and c = 49.

b² = 14² = 196

4ac = 4 * 1 * 49 = 196

Since, b² = 4ac is true here, x² + 14x + 49 is a perfect square trinomial.

To find the factors

x² + 14x + 49 = x(x+7) +7(x+7) = (x+7)²

As the factors are a perfect square, the expression x² + 14x + 49 is a perfect square trinomial.

How to use the perfect square trinomial checker?

The procedure to use the perfect square trinomial checker is as follows:

1Enter 3 numbers in the three input boxes respectively. If it is a negative number, remember to enter a negative sign before.
2Click Calculate button to verify whether the trinomial is a perfect square trinomial.
3Click the Reset button to start a new verification.

Solved examples using the perfect square trinomial checker

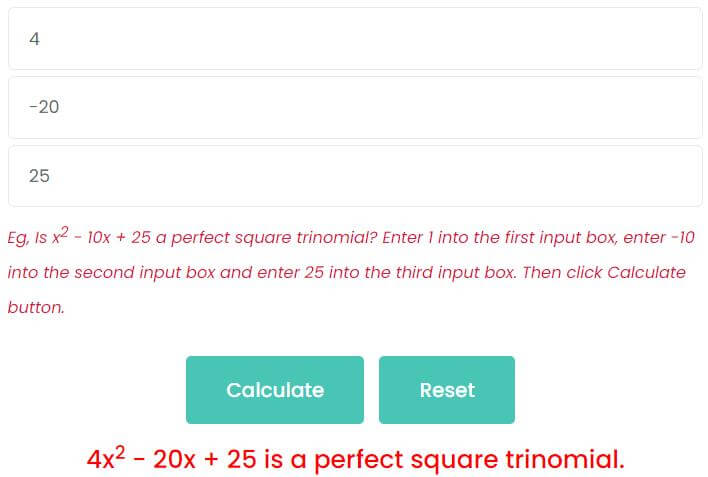
Example 1: Is 4x² – 20x + 25 a perfect square trinomial?

Enter 4 into the first input box.
Enter -20 into the second input box.
Enter 25 into the third input box.

Then click Calculate button, as shown in the figure, 4x² – 20x + 25 is a perfect square trinomial
.

4x² – 20x + 25 = (2x + 5)²

Is 4x^2 - 20x + 25 a perfect square trinomial?

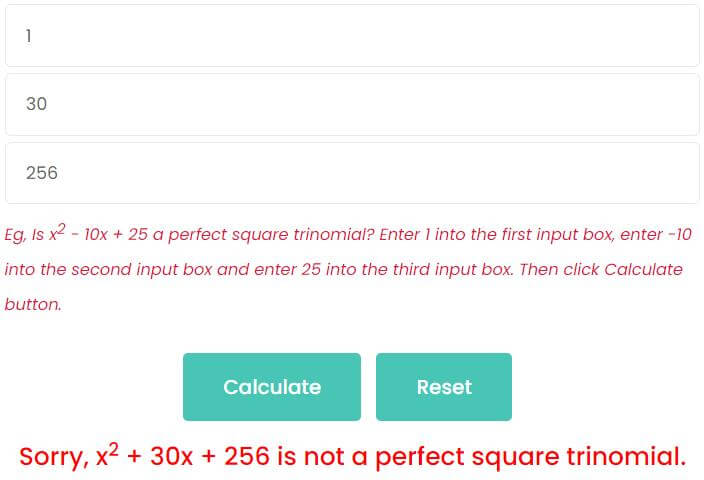
Example 2: Is x² + 30x + 256 a perfect square trinomial?

Enter 1 into the first input box.
Enter 30 into the second input box.
Enter 256 into the third input box.

Then click Calculate button, as shown in the figure, x² + 30x + 256 is not a perfect square trinomial. Here, a = 1, b = 30 and c = 256.
.

b² = 30² = 900

4ac = 4 * 1 * 256 = 1024

Since, b² is not equal to 4ac, x² + 30x + 256 is not a perfect square trinomial

Is x^2 + 30x + 256 a perfect square trinomial?

Perfect Square Trinomial Checker