The Odious Number Calculator is a free online tool used to check if the number is an odious number.
What is an odious number?
An odious number is a non-negative integer that has an odd number of 1s in its binary expansion. Therefore, to judge whether a positive integer is an odious number or not, two steps must be taken:
- Convert decimal integer to binary.
- Count the number of 1s in binary. If the number of 1s is odd, it is an odious number. If the number of 1s is even, it is an evil number.
For example, Is 360 an odious number?
First, Convert 360 to binary.
360 = 101101000
Obviously, there are 4 1s in binary. So, 360 is not an odious number.
First 100 odious numbers
| 1 | 2 | 4 | 7 | 8 | 11 | 13 | 14 | 16 | 19 |
| 21 | 22 | 25 | 26 | 28 | 31 | 32 | 35 | 37 | 38 |
| 41 | 42 | 44 | 47 | 49 | 50 | 52 | 55 | 56 | 59 |
| 61 | 62 | 64 | 67 | 69 | 70 | 73 | 74 | 76 | 79 |
| 81 | 82 | 84 | 87 | 88 | 91 | 93 | 94 | 97 | 98 |
| 100 | 103 | 104 | 107 | 109 | 110 | 112 | 115 | 117 | 118 |
| 121 | 122 | 124 | 127 | 128 | 131 | 133 | 134 | 137 | 138 |
| 140 | 143 | 145 | 146 | 148 | 151 | 152 | 155 | 157 | 158 |
| 161 | 162 | 164 | 167 | 168 | 171 | 173 | 174 | 176 | 179 |
| 181 | 182 | 185 | 186 | 188 | 191 | 193 | 194 | 196 | 199 |
How to use the odious number calculator
The procedure to use the odious number calculator is as follows:
- Enter the positive number.
- Click Calculate button to verify whether the input number is an odious number.
- Click the Reset button to start a new verification.
Solved examples using the odious number calculator
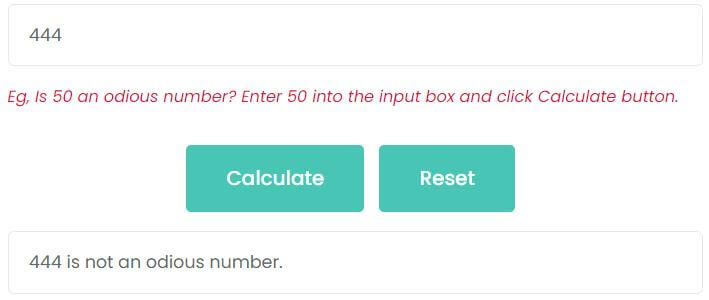
Example 1: Is 444 an odious number?
Enter 444 into the input box and click Calculate button, as shown in the figure, 444 is not an odious number.
444 = 110111100
The number of 1s is even. So, 444 is not an odious number, it is an evil number.
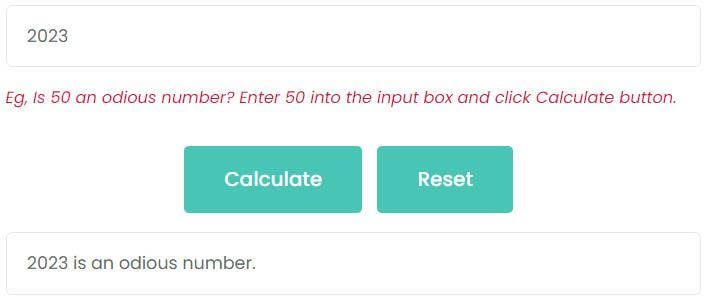
Example 2: Is 2023 an odious number?
Enter 2023 into the input box and click Calculate button, as shown in the figure, 2023 is an odious number.
2023 = 11111100111
There are 9 1s in binary. So, 2023 is an odious number.
Latest calculators
Standard Form to Slope-Intercept Form Calculator
Slope Intercept Form Calculator
Slope Calculator: Calculate Slope, X-Intercept, Y-Intercept
Reciprocal of Complex Number Calculator
Conjugate Complex Number Calculator
Modulus of Complex Number Calculator
Profit Percentage Calculator: Calculate Your Profitability Easily
Attendance and Absence Percentage Calculator
Circular Segment Radius Calculator
Regular Polygon Side Length Calculator
Annulus Calculator for Width, Perimeter, and Area