Median Absolute Deviation Calculator

Use this handy free calculator to calculate the median absolute deviation value. Multiple data can be entered at once, including integers, decimals and fractions. The value of the median absolute deviation is displayed in milliseconds.

The median absolute deviation, or MAD for short, is a robust measure of sample variability in a univariate dataset. It is more adaptable to outliers in the dataset than the standard deviation. For the standard deviation, the square of the distance from the data to the mean is used, so large deviations have more weight, and outliers can also have an important impact on the results. For MAD, a few outliers will not affect the final result.

Before calculating the median absolute deviation, give the formula first.

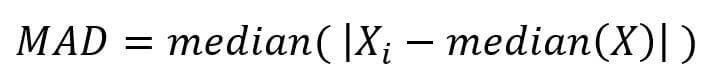Among them, X_i is each number in the dataset and median stands for taking the median.

For example, find the median absolute deviation for dataset {1, 2, 2, 6, 8, 10, 20, 25, 32}.

First, find the median of the dataset.

median(X) = 8

Second, calculate the absolute deviation for each number

X₁ = |1 – 8| = 7

X₂ = |2 – 8| = 6

X₃ = |2 – 8| = 6

X₄ = |6 – 8| = 2

X₅ = |8 – 8| = 0

X₆ = |10 – 8| = 2

X₇ = |20 – 8| = 12

X₈ = |25 – 8| = 17

X₉ = |32 – 8| = 24

Third, put the absolute deviation into a new data set and sort it

{7, 6, 6, 2, 0, 2, 12, 17, 24}

 

After sorting

 

{0, 2, 2, 6, 6, 7, 12, 17, 24}

The median of the new dataset is 6. So, the median absolute deviation for this dataset is 6.

Not sure how to find the median, click here for details

Many people confuse median absolute deviation with mean absolute deviation. Although they have the same abbreviation (MAD) and the latter contains the mean absolute deviation around the median, their meanings and calculations are completely different. The former takes the middle number at the end, and the latter finally takes the average. The mean absolute deviation covers a wider range, pay attention to respectively.

The Median Absolute Deviation Calculator is very simple to use. Enter data in the input box, you can enter multiple numbers at a time, and each number is separated by a comma or a new line. Whole numbers, decimals, or fractions are all fine. After input, click Calculate to get the value of the median absolute deviation.

There are two difficulties in calculating the median absolute deviation, one is to find the median, and the other is to calculate the absolute difference. If there is a tool that can perfectly solve these two problems, then the median absolute deviation can be easily obtained. The Median Absolute Deviation Calculator is born for this purpose, it is convenient and quick, suitable for anyone. Finally, everyone is welcome to use it.