Mean, Median, Mode, Quartile, Midrange and Range Calculator

Welcome to the free online calculator. The calculator is used to calculate the mean, median, mode, quartile, midrange, range, minimum, maximum and sum of a set of numbers.

The arithmetic mean, also known as the average, refers to the sum of a set of numbers divided by the total number of numbers in the set.

The arithmetic mean formula is

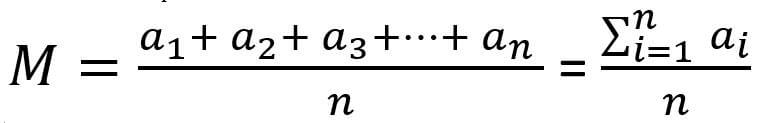For example, math grades in class 4 are 80, 85, 88, 92, 94, 89. What is the average score in math?

A total of 6 people, the sum of their scores is

80 + 85 + 88 + 92 + 94 + 89 = 528

So, their average score is

5286 = 88

The median, as the name suggests, is the number in the middle. A set of numbers, arranged in ascending order, the number in the middle is the median. If the middle position is not unique (the set has an even number of numbers), then take the average of the two middlemost values as the median.

For example, the median of a set of 1, 2, 3, 4, 5 is 3.

The median of a set of 1, 2, 3, 4, 5, 6 is

3 + 42 = 72 = 3.5

The mode is the value that occurs most frequently in the set. The mode can be one number or multiple numbers. If the numbers in the set all occur the same number of times, there is no mode.

For example, a set of numbers 1, 2, 3, 4, 5. All numbers appear once, so there is no mode.

Another set 1, 2, 3, 3, 4, 4, 5. The modes are 3 and 4. They both appear twice.

Arrange the values in the set from small to large and divide them into four equal parts. The values at the three dividing points are the quartiles. So, the quartile consists of 3 numbers: the first quartile, the second quartile and the third quartile, where the second quartile equals the median.

For example, a set of numbers 1, 2, 3, 4, 5, 6, 7.

The first quartile is 2, the second quartile is 4 and the third quartile is 6.

The midrange is the average of the maximum and minimum values of a set of numbers.

For example, the grades for the class are 66, 83, 72, 81, 96, 80, 55, 99, 60. What is the mid-range?

The highest score is 99, the lowest is 55. So, the midrange is

99 + 552 = 1542 = 77

A range is the difference between the maximum and minimum values of a set of numbers.

As in the example above, their range is 99 – 55 = 44.