Mean Absolute Deviation (MAD) Calculator - Average & Median

The Mean Absolute Deviation Calculator is a free online tool to calculate the mean absolute deviation of a dataset. Multiple data can be entered at once, including integers, decimals and fractions. There are two results shown, one is the mean absolute deviation around the mean and the other is the mean absolute deviation around the median.

In statistics, the mean absolute deviation is used to measure the dispersion of data. It is defined as the average of the absolute values of each data deviation from a central point. The center point can be the mean, median or mode. Among them, the mean absolute deviation around the mean and the mean absolute deviation around the median are more commonly used, and they can all be represented by MAD.

Formula for the mean absolute deviation around the mean

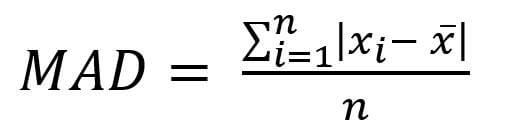Where n represents the length of data, x_i is each number in the data set and x is the mean.

Formula for the mean absolute deviation around the median

Where n represents the length of data, x_i is each number in the data set and m(x) is the median.

Click here to view the standard deviation.

Regardless of whether it is based on the mean or the median, at least the following steps need to be performed before the mean absolute deviation result can be obtained.

1. Find the average or median.
2. Compute Absolute Deviation.
3. Calculate the sum of absolute deviations.
4. Calculate the mean absolute deviation.

For example, find the mean absolute deviation around the mean for the dataset {2, 3, 5, 7, 8}.

First, calculate the mean

x = (2 + 3 + 5 + 7 + 8)5 = 255 = 5

Second, absolute deviation for each number

x₁ = |2 – 5| = 3

x₂ = |3 – 5| = 2

x₃ = |5 – 5| = 0

x₄ = |7 – 5| = 2

x₅ = |8 – 5| = 3

Third, sum of all absolute deviations.

Sum = 3 + 2 + 0 + 2 + 3 = 10

Finally, divide by the total to get the mean absolute deviation.

MAD = 105 = 2

Therefore, the mean absolute deviation around the mean of this dataset is 2.

The same procedure is done for the mean absolute deviation around the median.

Mean Absolute Deviation represents the mean absolute deviation around the mean, with the average as the center point.

Median Absolute Deviation is the mean absolute deviation around the median, with the median as the center point.

Although their center points are different, they are both used to measure the dispersion of data. Of course, when the mean and median are equal, their results are consistent. But in many cases, they are not equal.

For the data set {2, 3, 5, 7, 8} mentioned above, the median is also 5, so the mean absolute deviation around the mean and the mean absolute deviation around the median are both 2.

If you change 8 to 18, then the mean of them is

2 + 3 + 5 + 7 + 185 = 7

The mean absolute deviation around the mean for {2, 3, 5, 7, 18} is

MAD = |2 – 7| + |3 – 7| + |5 – 7| + |7 – 7| + |18 – 7|5

= 5 + 4 + 2 + 0 + 115

= 4.4

At this point, the median is still 5, so the mean absolute deviation around the median for {2, 3, 5, 7, 18} is

MAD = |2 – 5| + |3 – 5| + |5 – 5| + |7 – 5| + |18 – 5|5

= 3 + 2 + 0 + 2 + 135

= 4

Obviously, they are not the same.

In order to use the Mean Absolute Deviation Calculator, first have your data ready. Then type them all into the input box provided by the calculator. Note that each number is separated by a comma or a new line. Numbers can be integers, decimals or fractions, as appropriate. Finally, click Calculate to get the values of the mean absolute deviation, including the mean absolute deviation around the mean and the mean absolute deviation around the median.

The mean absolute deviation is a very important concept in statistics and is often used in reality. But its cumbersome calculation process makes many people a headache. Trust our Mean Absolute Deviation Calculator to be of great help and its free and easy-to-use features will keep you coming back for more.