The LCM calculator is an online tool used to calculate the least common multiple of two or more than two numbers in a matter of seconds. Finding LCM is of vital importance in Maths that aims to find the common denominators so that addition, subtraction, simplification and comparison of fractions can be performed.
What is LCM?
LCM stands for Least Common Multiple. These are also names attributed to Least Common Multiple:
- Lowest Common Multiple (LCM)
- Smallest Common Divisor (SCD)
- Lowest Common Denominator (LCD)
- Least Common Factor (LCF)
Least common multiple or LCM is the smallest multiple, which is commonly shared by 2 or more than 2 numbers. For example: the common multiples of the numbers 4 and 6 are 12, 24, 36. Once you look at these, you’ll realize that the smallest multiple is; 12, which is the LCM of 4 and 6.
In Math, multiple stands for a digit, which can be divided without leaving behind any remainder. E.g.: the number 48 is the multiple of the number 24, and the best part is it’s also of 1, 2, 3, 4, 6, 8, 16, 24, 48.
A common multiple is one, which is shared by more than 2 numbers. For example: the numbers 6 and 9 have three common multiples: 18, 36 and 54.
How to use the least common multiple
Least common multiples (LCMs) are necessary when fractions need to be expressed in the same denomination. For example, to add 38 + 17 we need to find first the common denominator. So, we calculate the least common multiple of 8 and 7, which is 56. The fraction can then be converted to 2156 + 856 = 2956.
In Math problems where we pair 2 objects against each other, the LCM value is useful in optimizing the quantities of the given objects. As well as in Computer Science, the LCM helps in designing encoded messages using cryptography.
How to calculate the least common multiple
There are several ways to find the least common multiple of 2 or more given numbers, and you can use any one of them. Depending on a particular situation, each method has its own merits and you can decide which one to pursue at your own disposition.
1. Listing Multiples (Brute Force Method)
This involves listing all the multiples of all the given numbers until you have reached the matched integers. Then find the smallest number, which is on the list and this becomes the LCM.
Example: find the LCM of 12, 15 and 75.
Multiples of 12:
12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144, 156, 168, 180, 192, 204, 216, 228, 240, 252, 264, 276, 288, 300, 312, 324
Multiples of 15:
15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180, 195, 210, 225, 240, 255, 270, 285, 300, 315, 330
Multiples of 75:
75, 150, 225, 300, 375, 450
The smallest number, which is in all of the lists is 300.
LCM (12, 15, 75) = 300.
Note that this method of listing the multiples is an ideal strategy, if the numbers are fairly small, such as the given examples above. For larger numbers, it would be easier to use the prime factorization method as listed below.
2. Prime Factorization
This process requires that you find all the prime factors of each given numbers. List down all the prime numbers you find, as many times as you see them most often for any given number. Prime numbers are those numbers that have only 2 factors: 1 and the number itself). Multiply the 2 prime numbers, and the product will be the LCM.
Example 1: find the LCM of 90 and 300
Prime factorization of 90:
90 = 2 * 3 * 3 * 5
Prime factorization of 300:
300 = 2 * 2 * 3 * 5 * 5
Multiplying the list of prime numbers together as often as they occur, we get 2 * 2 * 3 * 3 * 5 * 5 = 900.
LCM (90, 300) = 900.
Example 2: find the LCM of 150 and 500
Prime factorization of 150:
150 = 2 * 3 * 5 * 5
Prime factorization of 500:
500 = 2 * 2 * 5 * 5 * 5
Multiplying the list of prime numbers together as often as they occur, we get 2 * 2 * 3 * 5 * 5 * 5= 1500
LCM (150, 500) = 1500.
Note: If two given numbers have no prime factors in common, you can find the LCM by multiplying the 2 numbers.
Example 3: find the LCM of 31 and 54
Prime factors of 31:
31 = 31 * 1
Prime factorization of 54:
54 = 2 * 3 * 3 * 3
31 and 54 do not have prime factors in common.
So, the least common multiple of 31 and 54 is 31 * 54 = 1674.
3. Cake or Ladder Method
This method uses division to enable us to find the LCM of the numbers for which it is required to be found. Using simple division, people find these methods the quickest and simplest way of finding LCM.
For example: find the LCM of 9, 15, 17 and 30
1. Write down the given numbers in a row.
2. Divide the above numbers by a prime one that can be easily divisible by 3 and write down the end-result and bring it down to the next layer. The number, which cannot be easily divided has to be just brought down.
3. Continue with the division. Next we divide using 5 as the prime number. When all the prime numbers that divide evenly you got the LCM.
Multiply the numbers, which are in the extreme left row by numbers, which are in the bottom row, ignoring the number 1. therefore: 3 * 5 * 3 * 17 * 2 = 1530
The LCM of 9, 15, 17 and 30 is 1530.
4. Greatest Common Divisor (GCD) Method
This process uses the GCD the greatest common divisor, or the greatest common factor (GCF), among other names. The formula to find the LCM using the GCD method is:
LCM(a, b) = (a * b)/GCD(a, b)
Example for 2 given numbers: find the LCM of 4 and 12
The GCD of 4 and 12 is 4.
Calculate the LCM by GCF Formula:
(4 * 12) / 4 = 48 / 4 = 12
So, the LCM of 4 and 12 is 12.
Example for 3 given numbers: find the LCM of 15, 24 and 30.
GCD(15, 24) = 3
LCM(15, 24) = (15 * 24) /3 = 360/3 = 120
GCD(120, 30) = 30
LCM(120, 30) = (120 * 30) /30 = 3600/30 = 120
So, LCM(15, 24, 30) = 120.
Bear in mind that it is not important which LCM you calculate first, as long as you use all the numbers and you follow all the procedures accurately.
You will notice that doing the calculations manually can be a daunting and tedious task. The least common multiple calculator will do all the work in a fraction of a second.
How to use the LCM calculator
Using the LCM Calculator is a simple and easy process. Just follow the following steps.
- Enter the values on the input box, using a comma to separate each values.
- Press the “Calculate” button, you will get the least common multiple of the given numbers.
- Press the “Reset” button to get ready for another calculation.
When doing a manual calculation, you will notice that the methods are a bit complicated and thus confusing. So why insist on doing it when you can easily get results by simply using the LCM calculator. Experience the ease of using this calculator, as it is simple and hassle free to use, and you can add it on your online platforms.
Next, let’s take a few examples to see how this calculator is used.
Solved examples using LCM calculator
Find the LCM of 2 numbers
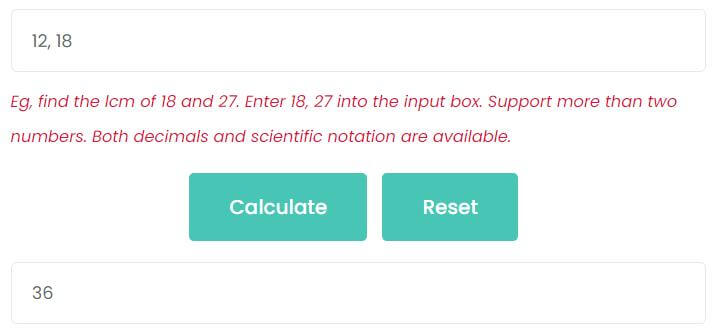
For example, find the LCM of 12 and 18.
Enter 12, 18 on the input box, then click Calculate button. As the picture shows, the least common multiple of 12 and 18 is 36.
Find the LCM of 3 numbers
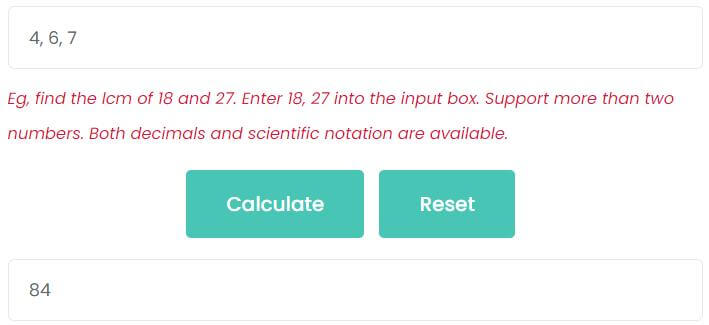
For example, find the LCM of 4, 6 and 7.
Enter 4, 6, 7 on the input box, then click Calculate button. As the picture shows, the least common multiple of 4, 6 and 7 is 84.
Find the LCM of 4 or more numbers
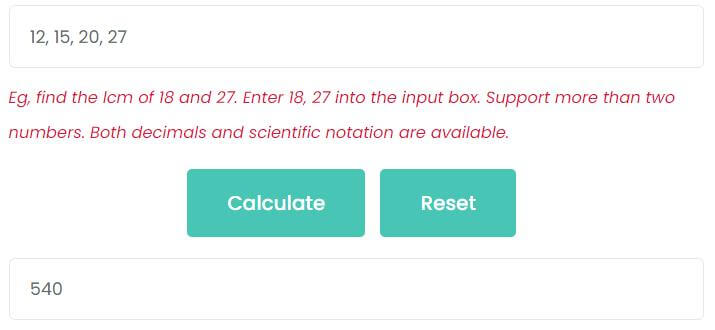
For example, find the LCM of 12, 15, 20 and 27.
Enter 12, 15, 20, 27 on the input box, then click Calculate button. As the picture shows, the least common multiple of 12, 15, 20 and 27 is 540.
Latest calculators
Standard Form to Slope-Intercept Form Calculator
Slope Intercept Form Calculator
Slope Calculator: Calculate Slope, X-Intercept, Y-Intercept
Reciprocal of Complex Number Calculator
Conjugate Complex Number Calculator
Modulus of Complex Number Calculator
Profit Percentage Calculator: Calculate Your Profitability Easily
Attendance and Absence Percentage Calculator
Circular Segment Radius Calculator
Regular Polygon Side Length Calculator
Annulus Calculator for Width, Perimeter, and Area