Law of Cosines Calculator

Find Triangle Sides and Angles

Have you ever wondered how to solve complex triangle problems with ease? Look no further, as we introduce you to the powerful Law of Cosines calculator. In this article, we’ll explore the ins and outs of the Law of Cosines, guide you through the step-by-step process of using the calculator, and provide solved examples to deepen your understanding. Get ready to unravel the mysteries of triangles and become a master of trigonometry!

Law of Cosines Calculator

Enter at least 3 values, and they cannot all be angles.

Calculate Reset

What is the Law of Cosines

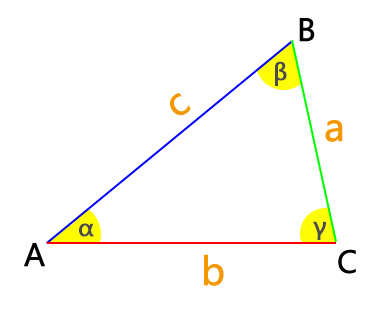
The Law of Cosines is a fundamental principle in trigonometry that allows us to calculate the lengths of sides and measures of angles in a triangle. It extends the Pythagorean theorem to all types of triangles, not just right triangles. In simple terms, the Law of Cosines relates the lengths of the sides of a triangle to the cosine of one of its angles.

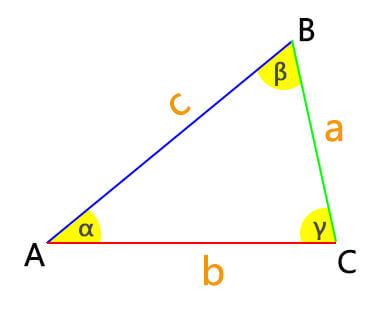triangle The formula for the Law of Cosines is as follows:

c² = a² + b² – 2ab * cos(C)

Here, c represents the length of the side opposite angle C, while a and b are the lengths of the other two sides. The angle C is the angle opposite side c. By utilizing this formula, we can find missing side lengths or angle measures in a triangle when provided with certain information.

For Other Sides

b² = a² + c² – 2ac * cos(B)

a² = b² + c² – 2bc * cos(A)

for Angles

A = arccos(b² + c² – a²2bc)

B = arccos(a² + c² – b²2ac)

C = arccos(a² + b² – c²2ab)

For example, Let’s consider a triangle with side lengths a = 5 units, b = 7 units, and an included angle C = 60 degrees. We want to find the length of the third side c.

Step 1: Gather the required information

We have the lengths of two sides (a = 5, b = 7) and the measure of the included angle C (60 degrees).

Step 2: Identify the known values

In our example, a = 5, b = 7, and C = 60°.

Step 3: Select the appropriate formula

We will use the Law of Cosines formula to calculate the unknown side c:

c² = a² + b² – 2ab * cos(C)

Step 4: Plug in the values and calculate

Substituting the known values into the formula, we have:

c² = 5² + 7² – 2 * 5 * 7 * cos(60°)

Calculating further:

c² = 25 + 49 – 70 * cos(60°)

c² = 74 – 70 * 0.5

c² = 74 – 35

c² = 39

Taking the square root of both sides, we find:

c = √39 = 6.24

Step 5: Repeat if necessary

In this example, we have found the length of side c. If we needed to find other unknown sides or angles, we would repeat steps 3 and 4 using the appropriate formula and known values.

So, in our triangle, the length of side c is approximately 6.24 units.

What is the Law of Cosines Calculator

like the law of sines calculator， the Law of Cosines Calculator is a valuable tool that automates the process of applying the Law of Cosines to solve triangle problems. With its user-friendly interface and efficient calculations, it simplifies complex trigonometric calculations, saving you time and effort.

How to Use the Law of Cosines Calculator

Follow these steps to harness the power of the Law of Cosines Calculator:

1Enter the known values into the corresponding fields, such as side lengths or angle measures. At least 3 values must be entered, and these 3 values cannot all be angles.
2Select the angle type, degrees or radians, the default is degrees.
3Click the Calculate button to obtain the result.
4Click the Reset button to start a new calculation

The calculator will provide you with the missing side length or angle measure, allowing you to solve even the most intricate triangle problems effortlessly.

FAQs

Q: What is the Law of Cosines?
A: The Law of Cosines is a trigonometric formula used to find the lengths of the sides or measures of the angles of a triangle. It relates the lengths of the sides of a triangle to the cosine of one of its angles.

Q: When should I use the Law of Cosines?
A: You should use the Law of Cosines when you have enough information about a triangle, such as the lengths of two sides and the measure of the included angle, and you want to find the length of the third side or the measures of the remaining angles.

Q: Can the Law of Cosines be used for any type of triangle?
A: Yes, the Law of Cosines can be used for any type of triangle, whether it is an acute triangle, obtuse triangle, or right triangle. However, for right triangles, the Pythagorean theorem is often more convenient to use.

Q: What if I don't know the measure of the included angle?
A: If you don’t know the measure of the included angle, you can also calculate the angles by directly entering the lengths of the 3 sides.

Q: What is the difference between the Law of Cosines and the Pythagorean theorem?
A: While the Pythagorean theorem is applicable only to right triangles, the Law of Cosines is more general and can be used for any type of triangle. The Law of Cosines accounts for all three sides and angles of a triangle, allowing us to find missing side lengths or angle measures.

Q: How does the Law of Cosines apply to real-life scenarios?
A: The Law of Cosines has various applications in real-life scenarios, particularly in fields such as architecture, engineering, navigation, and physics. It can be used to determine distances, angles, and forces in triangular structures, navigation calculations, satellite positioning, and more.

Q: Is there a way to simplify the Law of Cosines formula?
A: The Law of Cosines formula is a fundamental mathematical expression that relates the lengths of sides and measures of angles in a triangle. While the formula itself cannot be simplified, using a calculator or software can make the calculations easier and faster. Just like the law of cosines calculator available on our page.

Q: Are there alternative methods for solving triangles?
A: Yes, there are alternative methods for solving triangles, such as the Law of Sines and the use of trigonometric functions like sine, cosine, and tangent. These methods depend on the given information and the specific problem at hand. The choice of method often depends on the available information and the desired unknowns to be calculated.

Conclusion

Congratulations! You’ve delved into the intricacies of the Law of Cosines and discovered the power of the Law of Cosines Calculator. With this newfound knowledge, you can confidently tackle triangle problems and unlock a world of possibilities in trigonometry. Remember, practice makes perfect, so keep exploring different scenarios and expanding your skills. Embrace the Law of Cosines, and let your triangle-solving prowess soar!