Welcome to the Isosceles Triangle Calculator – this tool is designed to make calculations of sides, angles, height, perimeter, and area a breeze.
What is an Isosceles Triangle
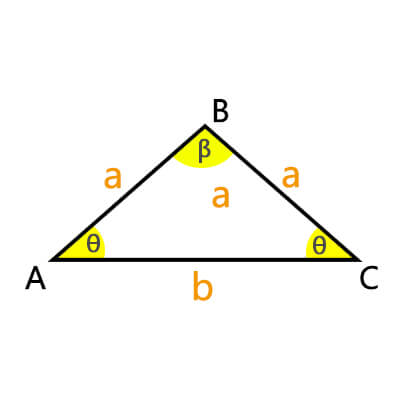
 An isosceles triangle is a unique geometric figure characterized by having two sides of equal length, forming two equal angles. The third side is of a different length, creating a sense of symmetry. If the third side is also of the same length, it becomes an equilateral triangle.Understanding the properties of isosceles triangles opens a door to a captivating realm of geometry.
An isosceles triangle is a unique geometric figure characterized by having two sides of equal length, forming two equal angles. The third side is of a different length, creating a sense of symmetry. If the third side is also of the same length, it becomes an equilateral triangle.Understanding the properties of isosceles triangles opens a door to a captivating realm of geometry.
How to Calculate the Sides, Angles, Height, Perimeter, or Area
Let’s unravel the magic of isosceles triangles through the Isosceles Triangle Calculator, offering step-by-step instructions for calculating various parameters.
Given Two Sides: (Waist Side and Bottom Side)
Denoted as the waist side (a), the bottom side (b), and the other side(c).
1. Calculate the Other Side:
In an isosceles triangle, the other side (c) is equal to the waist side (a). Therefore
c = a
2. Calculate Angles:
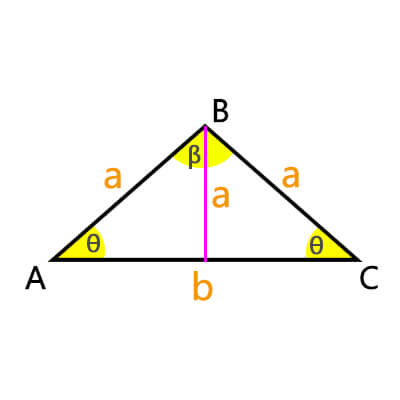
Determine the two equal angles (θ) using trigonometric ratios. The height on the bottom side is also the center line on the bottom edge. Calculate for equal angles using arc cosine:
θ = arccos(b/2a)
3. Calculate Perimeter:
Find the perimeter (P) by summing the three sides:
P = a + b + c
which simplifies to
P = a + b + a = 2a + b
4. Calculate Area:
Utilize Heron’s formula for the area (A):
A= √(s * (s – a) * (s – b) * (s – c))
Where, s is the semi-perimeter. In this case
s = (2a+b)/2 = a+ b/2
5. Calculate Height:
The height (h) of the isosceles triangle can be found using
h = √(a2 – (b2/4))
Example, The waist length of an isosceles triangle is a = 4units and the base length is b = 6 units.
The equal angles are
θ = arccos(b/2a) = arccos(6 / 2 * 4) = arccos(3 / 4) = 41.4 degrees
The vertex angle is
180 – 2θ = 180 – 2 * 41.4 = 97.2 degrees
The perimeter is
P = 2a + b = 2 * 4 + 6 = 14 units
The semi-perimeter is
s = P/2 = 14 /2 = 7 units
The area is
A = √(s * (s – a) * (s – b) * (s – c))
A = √(7 * (7 – 4) * (7 – 6) * (7 – 4))
A = √(7 * 3 * 1 * 3)
A = √42
A = 7.937 square units
The height is
h = √(a2 – (b2/4)) = √(42 – (62/4)) = 2.65 units
Given One Angle and One Side:
Let’s work through the scenario where you have one angle and one side in an isosceles triangle. First, we need to determine whether the given angle is a base angle or a vertex angle. Then, we can use the fact that the sum of the interior angles of a triangle is equal to 180 degrees to calculate the three angles of the isosceles triangle.
1. Calculate Angles:
If the given angle (θ) is one of the base angles, then the other base angle is also θ since an isosceles triangle has two equal angles. The vertex angle is
180 – 2θ
If the given angle (θ) is the vertex angle (angle between the two equal sides), then the base angles are also:
(180 – θ)/2
2. Calculate Other Sides:
Now you know the three angles and one side of an isosceles triangle, and you want to calculate the other two sides (b and c) using the sine theorem.
B = a*sin(b)/sin(a)
C = a *sin(c)/sin(a)
3. Calculate Perimeter, Area and Height:
Once you know the three angles and three sides of an isosceles triangle, you can easily calculate the perimeter, area, and height of the isosceles triangle. See method one for details.
FAQs
- Q: Can an isosceles triangle have three equal angles?A: No, an isosceles triangle has two equal angles, making the third angle different.If the third angle is also the same, it becomes an equilateral triangle.
- Q: Can I use the Isosceles Triangle Calculator for any triangle?A: No, this calculator is specifically designed for isosceles triangles.
- Q: How is the height of an isosceles triangle calculated?A: The height can be found using h= √(a2 – (b2/4)), where a is the equal side and b is the third side.
- Q: How do I input decimal values in the calculator?A: Simply use a dot (.) for decimal points, e.g., 7.5.
- Q: Is the calculator suitable for beginners?A: Yes, the step-by-step instructions make it user-friendly, even for those new to geometry.
- Q: Can I use the Isosceles Triangle Calculator for right-angled triangles?A: While the calculator is specialized for isosceles triangles, it can handle right-angled triangles as long as the given information aligns with isosceles properties.
- Q: Can the calculator handle negative values?A: No. The Isosceles Triangle Calculator is designed for positive values.
- Q: Is the calculator suitable for academic or professional use?A: Yes, the Isosceles Triangle Calculator is versatile enough for both academic learning and professional applications. It provides accurate results for various scenarios.
- Q: Can I use the Isosceles Triangle Calculator for triangles with acute or obtuse angles?A: The calculator is specifically designed for isosceles triangles, which can have acute, obtuse, or right angles. It accommodates various triangle scenarios within the isosceles framework.
Latest Calculators
Standard Form to Slope-Intercept Form Calculator
Slope Intercept Form Calculator
Slope Calculator: Calculate Slope, X-Intercept, Y-Intercept
Reciprocal of Complex Number Calculator
Conjugate Complex Number Calculator
Modulus of Complex Number Calculator
Profit Percentage Calculator: Calculate Your Profitability Easily
Attendance and Absence Percentage Calculator
Trigonometric Functions
Arccsc Calculator – Find the Exact Value of Inverse Cosecant
Arcsec Calculator – Find the Exact Value of Inverse Secant
Arccot Calculator – Find the Exact Value of Inverse Cotangent
Arctan Calculator – Find the Exact Value of Inverse Tangent
Inverse Cosine Calculator – Find The Exact Value of Arccos
Inverse Sine Calculator – Find The Exact Value of Arcsin
Inverse Trigonometric Functions Calculator
Trigonometric Functions Conversion Calculator
Trig Calculator – Find 6 Trigonometric Functions by Angles or Sides