Inverse Sine Calculator is a free online tool to calculate the exact value of arcsin in degrees or radians.
What is arcsin?
Arcsine is an inverse trigonometric function, which refers to the inverse function of sine within -π2 to π2. Denoted as arcsin or sin-1. It is used to find angles based on the trigonometric ratio of the opposite side to the hypotenuse. Therefore, the formula for arcsine is:
sin(θ) = oppositehypotenuse
θ = arcsin(oppositehypotenuse)
If the sine function is represented by x and y (as follows)
y = sin(x), x∈[-π2, π2]
Then, the arcsine function can be expressed as:
x = arcsin(y), y∈[-1, 1]
In order to conform to the habit, define x as a variable and y as a dependent variable, so the arcsine function can be replaced by
y = arcsin(x), x ∈[-1, 1], y∈[-π2, π2]
Since sine is a periodic function, there cannot be a single-valued inverse function in the domain of sine. Therefore, the domain of the arcsine function can only be limited to the interval [-1, 1]. In this range, x and y are in one-to-one correspondence.
Arcsin graph and properties
Like sine, connecting each point of arcsine will form a smooth curve, as follows
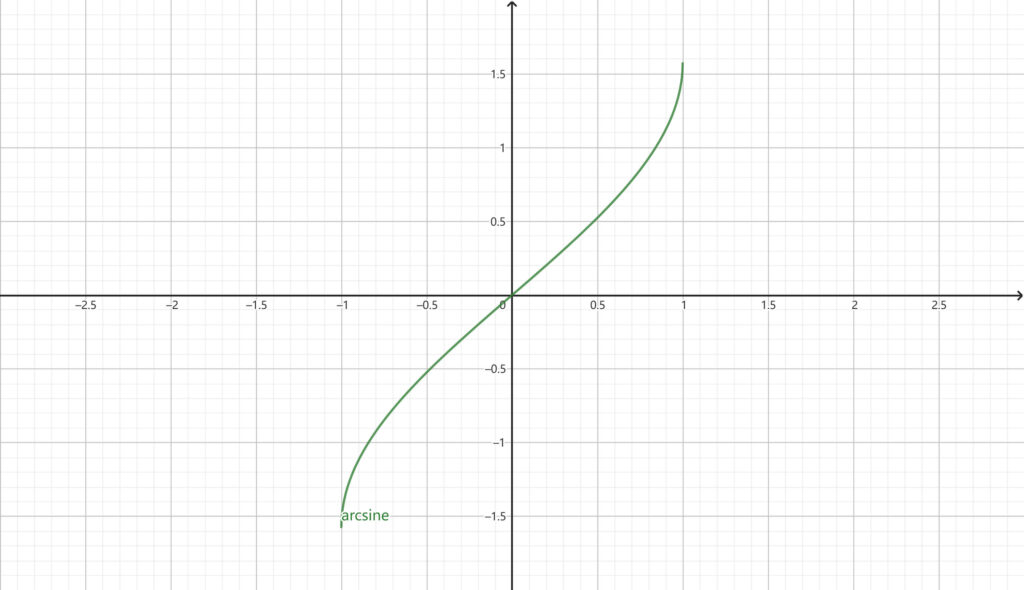
arcsin graph
Through this curve, we can summarize several characteristics of arcsine
- Domain – The domain of arcsine is between -1 and 1.
- Range – The range of arcsine is -π2 to π2.
- Monotonicity – In the domain, the arcsine increases monotonically
- Odd function – Since arcsin(x) = – arcsin (-x), arcsin is an odd function.
How to calculate arcsine?
Computing the arcsine by hand is uncommon, usually only some commonly used arcsines are computed.
For example
sin(30°) = 0.5. So, arcsin(0.5) = 30°
sin(90°) = 1. Thus, arcsin(1) = 90°
For some unfamiliar values, calculating the arcsine requires the help of an arcsine table or an arcsine calculator. The arcsine table (given below) lists the corresponding relationship between the sine value and the angle, which is convenient for finding the arcsine value. The disadvantage is that the numbers listed in the arcsine table are limited, and some uncommon values may not be found. So, it is recommended to use the arcsine calculator on this page so that you can easily find all arcsine values.
| arcsine(x) | Degrees | Radians |
| -1 | -90° | -π2 |
| -0.9998477 | -89° | -89π180 |
| -0.99939083 | -88° | -22π45 |
| -0.99862953 | -87° | -29π60 |
| -0.99756405 | -86° | -43π90 |
| -0.9961947 | -85° | -17π36 |
| -0.9945219 | -84° | -7π15 |
| -0.99254615 | -83° | -83π180 |
| -0.99026807 | -82° | -41π90 |
| -0.98768834 | -81° | -9π20 |
| -0.98480775 | -80° | -4π9 |
| -0.98162718 | -79° | -79π180 |
| -0.9781476 | -78° | -13π30 |
| -0.97437006 | -77° | -77π180 |
| -0.97029573 | -76° | -19π45 |
| -0.96592583 | -75° | -5π12 |
| -0.9612617 | -74° | -37π90 |
| -0.95630476 | -73° | -73π180 |
| -0.95105652 | -72° | -2π5 |
| -0.94551858 | -71° | -71π180 |
| -0.93969262 | -70° | -7π18 |
| -0.93358043 | -69° | -23π60 |
| -0.92718385 | -68° | -17π45 |
| -0.92050485 | -67° | -67π180 |
| -0.91354546 | -66° | -11π30 |
| -0.90630779 | -65° | -13π36 |
| -0.89879405 | -64° | -16π45 |
| -0.89100652 | -63° | -7π20 |
| -0.88294759 | -62° | -31π90 |
| -0.87461971 | -61° | -61π180 |
| -0.8660254 | -60° | -1π3 |
| -0.8571673 | -59° | -59π180 |
| -0.8480481 | -58° | -29π90 |
| -0.83867057 | -57° | -19π60 |
| -0.82903757 | -56° | -14π45 |
| -0.81915204 | -55° | -11π36 |
| -0.80901699 | -54° | -3π10 |
| -0.79863551 | -53° | -53π180 |
| -0.78801075 | -52° | -13π45 |
| -0.77714596 | -51° | -17π60 |
| -0.76604444 | -50° | -5π18 |
| -0.75470958 | -49° | -49π180 |
| -0.74314483 | -48° | -4π15 |
| -0.7313537 | -47° | -47π180 |
| -0.7193398 | -46° | -23π90 |
| -0.70710678 | -45° | -1π4 |
| -0.69465837 | -44° | -11π45 |
| -0.68199836 | -43° | -43π180 |
| -0.66913061 | -42° | -7π30 |
| -0.65605903 | -41° | -41π180 |
| -0.64278761 | -40° | -2π9 |
| -0.62932039 | -39° | -13π60 |
| -0.61566148 | -38° | -19π90 |
| -0.60181502 | -37° | -37π180 |
| -0.58778525 | -36° | -1π5 |
| -0.57357644 | -35° | -7π36 |
| -0.5591929 | -34° | -17π90 |
| -0.54463904 | -33° | -11π60 |
| -0.52991926 | -32° | -8π45 |
| -0.51503807 | -31° | -31π180 |
| -0.5 | -30° | -1π6 |
| -0.48480962 | -29° | -29π180 |
| -0.46947156 | -28° | -7π45 |
| -0.4539905 | -27° | -3π20 |
| -0.43837115 | -26° | -13π90 |
| -0.42261826 | -25° | -5π36 |
| -0.40673664 | -24° | -2π15 |
| -0.39073113 | -23° | -23π180 |
| -0.37460659 | -22° | -11π90 |
| -0.35836795 | -21° | -7π60 |
| -0.34202014 | -20° | -1π9 |
| -0.32556815 | -19° | -19π180 |
| -0.30901699 | -18° | -1π10 |
| -0.2923717 | -17° | -17π180 |
| -0.27563736 | -16° | -4π45 |
| -0.25881905 | -15° | -1π12 |
| -0.2419219 | -14° | -7π90 |
| -0.22495105 | -13° | -13π180 |
| -0.20791169 | -12° | -1π15 |
| -0.190809 | -11° | -11π180 |
| -0.17364818 | -10° | -1π18 |
| -0.15643447 | -9° | -1π20 |
| -0.1391731 | -8° | -2π45 |
| -0.12186934 | -7° | -7π180 |
| -0.10452846 | -6° | -1π30 |
| -0.08715574 | -5° | -1π36 |
| -0.06975647 | -4° | -1π45 |
| -0.05233596 | -3° | -1π60 |
| -0.0348995 | -2° | -1π90 |
| -0.01745241 | -1° | -1π180 |
| 0 | 0° | 0 |
| 0.01745241 | 1° | π180 |
| 0.0348995 | 2° | π90 |
| 0.05233596 | 3° | π60 |
| 0.06975647 | 4° | π45 |
| 0.08715574 | 5° | π36 |
| 0.10452846 | 6° | π30 |
| 0.12186934 | 7° | 7π180 |
| 0.1391731 | 8° | 2π45 |
| 0.15643447 | 9° | π20 |
| 0.17364818 | 10° | π18 |
| 0.190809 | 11° | 11π180 |
| 0.20791169 | 12° | π15 |
| 0.22495105 | 13° | 13π180 |
| 0.2419219 | 14° | 7π90 |
| 0.25881905 | 15° | π12 |
| 0.27563736 | 16° | 4π45 |
| 0.2923717 | 17° | 17π180 |
| 0.30901699 | 18° | π10 |
| 0.32556815 | 19° | 19π180 |
| 0.34202014 | 20° | π9 |
| 0.35836795 | 21° | 7π60 |
| 0.37460659 | 22° | 11π90 |
| 0.39073113 | 23° | 23π180 |
| 0.40673664 | 24° | 2π15 |
| 0.42261826 | 25° | 5π36 |
| 0.43837115 | 26° | 13π90 |
| 0.4539905 | 27° | 3π20 |
| 0.46947156 | 28° | 7π45 |
| 0.48480962 | 29° | 29π180 |
| 0.5 | 30° | π6 |
| 0.51503807 | 31° | 31π180 |
| 0.52991926 | 32° | 8π45 |
| 0.54463904 | 33° | 11π60 |
| 0.5591929 | 34° | 17π90 |
| 0.57357644 | 35° | 7π36 |
| 0.58778525 | 36° | π5 |
| 0.60181502 | 37° | 37π180 |
| 0.61566148 | 38° | 19π90 |
| 0.62932039 | 39° | 13π60 |
| 0.64278761 | 40° | 2π9 |
| 0.65605903 | 41° | 41π180 |
| 0.66913061 | 42° | 7π30 |
| 0.68199836 | 43° | 43π180 |
| 0.69465837 | 44° | 11π45 |
| 0.70710678 | 45° | π4 |
| 0.7193398 | 46° | 23π90 |
| 0.7313537 | 47° | 47π180 |
| 0.74314483 | 48° | 4π15 |
| 0.75470958 | 49° | 49π180 |
| 0.76604444 | 50° | 5π18 |
| 0.77714596 | 51° | 17π60 |
| 0.78801075 | 52° | 13π45 |
| 0.79863551 | 53° | 53π180 |
| 0.80901699 | 54° | 3π10 |
| 0.81915204 | 55° | 11π36 |
| 0.82903757 | 56° | 14π45 |
| 0.83867057 | 57° | 19π60 |
| 0.8480481 | 58° | 29π90 |
| 0.8571673 | 59° | 59π180 |
| 0.8660254 | 60° | π3 |
| 0.87461971 | 61° | 61π180 |
| 0.88294759 | 62° | 31π90 |
| 0.89100652 | 63° | 7π20 |
| 0.89879405 | 64° | 16π45 |
| 0.90630779 | 65° | 13π36 |
| 0.91354546 | 66° | 11π30 |
| 0.92050485 | 67° | 67π180 |
| 0.92718385 | 68° | 17π45 |
| 0.93358043 | 69° | 23π60 |
| 0.93969262 | 70° | 7π18 |
| 0.94551858 | 71° | 71π180 |
| 0.95105652 | 72° | 2π5 |
| 0.95630476 | 73° | 73π180 |
| 0.9612617 | 74° | 37π90 |
| 0.96592583 | 75° | 5π12 |
| 0.97029573 | 76° | 19π45 |
| 0.97437006 | 77° | 77π180 |
| 0.9781476 | 78° | 13π30 |
| 0.98162718 | 79° | 79π180 |
| 0.98480775 | 80° | 4π9 |
| 0.98768834 | 81° | 9π20 |
| 0.99026807 | 82° | 41π90 |
| 0.99254615 | 83° | 83π180 |
| 0.9945219 | 84° | 7π15 |
| 0.9961947 | 85° | 17π36 |
| 0.99756405 | 86° | 43π90 |
| 0.99862953 | 87° | 29π60 |
| 0.99939083 | 88° | 22π45 |
| 0.9998477 | 89° | 89π180 |
| 1 | 90° | π2 |
How to use this inverse sine calculator
Arcsine Calculator is so easy to use, even for kids. Enter the sine value, and then click the Calculate button to find the arcsine value, which is the angle. By default, the degrees and radians of the angle will be displayed. Note that the range of input values is between -1 and 1. Decimals and fractions are also supported.
FAQS
- Q: What is inverse sine used for?A: Arcsine is used to find the corresponding angle based on the sine value.
- Q: Are arcsin and sin^-1 the same?A: Yes, they are the same, both represent arcsine.
- Q: Are arcsin and csc the same?A: No. They are different, arcsin is the inverse function of sine, and csc is the reciprocal of sine.
- Q: What is the output of the arcsine calculator?A: The output of the arcsine calculator is an angle, which can be in degrees or radians.
- Q: What is the derivative of arcsine?A: The derivative of arcsine is 1√(1-x2)
(arcsin(x))’ = 1√(1-x2)
Conclusion
In summary, arcsine is a very important inverse trigonometric function. When the sine value is known, the angle value can be easily calculated by the arcsine function. If you don’t know how to calculate it, just use our arcsine calculator. One second to input, one second to get an answer.
Latest Calculators
Standard Form to Slope-Intercept Form Calculator
Slope Intercept Form Calculator
Slope Calculator: Calculate Slope, X-Intercept, Y-Intercept
Reciprocal of Complex Number Calculator
Conjugate Complex Number Calculator
Modulus of Complex Number Calculator
Profit Percentage Calculator: Calculate Your Profitability Easily
Attendance and Absence Percentage Calculator
Trigonometric Functions
Arccsc Calculator – Find the Exact Value of Inverse Cosecant
Arcsec Calculator – Find the Exact Value of Inverse Secant
Arccot Calculator – Find the Exact Value of Inverse Cotangent
Arctan Calculator – Find the Exact Value of Inverse Tangent
Inverse Cosine Calculator – Find The Exact Value of Arccos
Inverse Trigonometric Functions Calculator
Trigonometric Functions Conversion Calculator
Trig Calculator – Find 6 Trigonometric Functions by Angles or Sides