Inverse Cosine Calculator – Find The Exact Value of Arccos

The Inverse Cosine Calculator is a handy online tool for finding the exact value of the arccos.

Inverse Cosine Calculator

What is arccos?

Arccosine is the inverse function of cosine and is used to find the measure of angles in a right triangle based on the ratio of the adjacent side to the hypotenuse. Arccosine is an inverse trigonometric function. The mathematical symbol for arccosine is arccos, often denoted as cos^-1.

The arccosine formula is

θ = arccos(oppositehypotenuse)

Arccos graph and properties

Since the range of cosine is between -1 and 1, the domain of arccosine is also defined between -1 and 1. To avoid the periodicity of cosine (multiple angles correspond to one value), it is impossible to have an inverse function. Therefore, the value range of arccosine is specified between 0 and π. The graph of the arccosine is as follows:

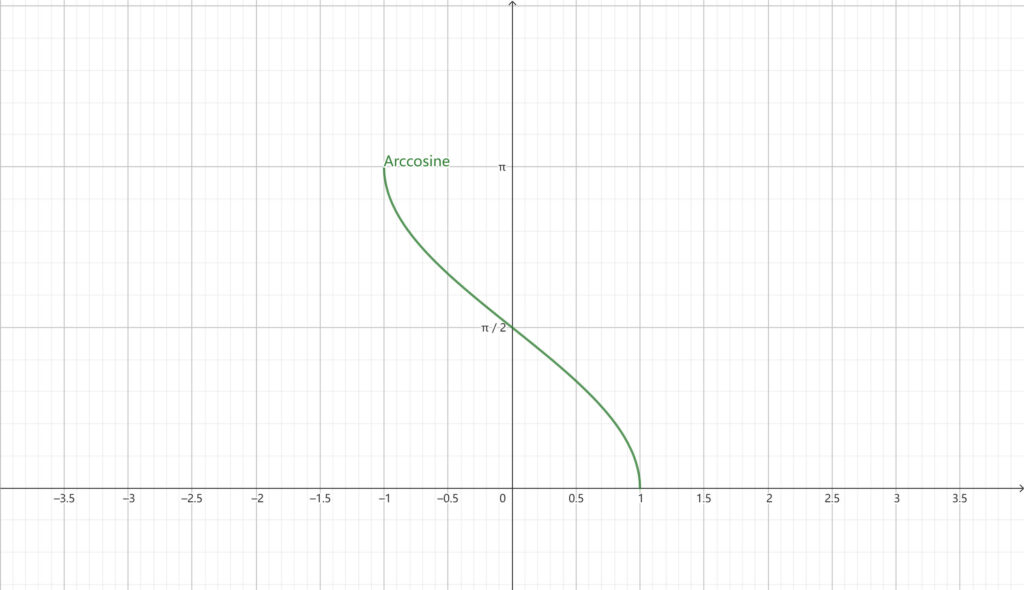
Arccosine graph

Domain – The domain of arccosine is between -1 and 1.
Range – The range of arccosine is 0 to π.
Monotonicity – In the domain, the arccosine monotonically decreasing
Neither odd nor even function – Because arccos(x) ≠ arccos(-x), arccosine is not an even function. At the same time, arccos(x) ≠ -arccos(-x), so arccosine is not an odd function.

How to calculate arccos?

There are two ways to calculate the arccosine. One is the traditional method. Use the arccosine table to find the correspondence between the cosine value and the angle. The other is an easy way to use the arccosine calculator to calculate the value of the arccosine. Clearly, an arccosine calculator has advantages over an arccosine table. The arccosine calculator can calculate the answer in milliseconds. If you want to use the traditional method, please refer to our arccosine table below.

arccos(x)	Degrees	Radians
1	0°	0
0.9998477	1°	π180
0.99939083	2°	π90
0.99862953	3°	π60
0.99756405	4°	π45
0.9961947	5°	π36
0.9945219	6°	π30
0.99254615	7°	7π180
0.99026807	8°	2π45
0.98768834	9°	π20
0.98480775	10°	π18
0.98162718	11°	11π180
0.9781476	12°	π15
0.97437006	13°	13π180
0.97029573	14°	7π90
0.96592583	15°	π12
0.9612617	16°	4π45
0.95630476	17°	17π180
0.95105652	18°	π10
0.94551858	19°	19π180
0.93969262	20°	π9
0.93358043	21°	7π60
0.92718385	22°	11π90
0.92050485	23°	23π180
0.91354546	24°	2π15
0.90630779	25°	5π36
0.89879405	26°	13π90
0.89100652	27°	3π20
0.88294759	28°	7π45
0.87461971	29°	29π180
0.8660254	30°	π6
0.8571673	31°	31π180
0.8480481	32°	8π45
0.83867057	33°	11π60
0.82903757	34°	17π90
0.81915204	35°	7π36
0.80901699	36°	π5
0.79863551	37°	37π180
0.78801075	38°	19π90
0.77714596	39°	13π60
0.76604444	40°	2π9
0.75470958	41°	41π180
0.74314483	42°	7π30
0.7313537	43°	43π180
0.7193398	44°	11π45
0.70710678	45°	π4
0.69465837	46°	23π90
0.68199836	47°	47π180
0.66913061	48°	4π15
0.65605903	49°	49π180
0.64278761	50°	5π18
0.62932039	51°	17π60
0.61566148	52°	13π45
0.60181502	53°	53π180
0.58778525	54°	3π10
0.57357644	55°	11π36
0.5591929	56°	14π45
0.54463904	57°	19π60
0.52991926	58°	29π90
0.51503807	59°	59π180
0.5	60°	π3
0.48480962	61°	61π180
0.46947156	62°	31π90
0.4539905	63°	7π20
0.43837115	64°	16π45
0.42261826	65°	13π36
0.40673664	66°	11π30
0.39073113	67°	67π180
0.37460659	68°	17π45
0.35836795	69°	23π60
0.34202014	70°	7π18
0.32556815	71°	71π180
0.30901699	72°	2π5
0.2923717	73°	73π180
0.27563736	74°	37π90
0.25881905	75°	5π12
0.2419219	76°	19π45
0.22495105	77°	77π180
0.20791169	78°	13π30
0.190809	79°	79π180
0.17364818	80°	4π9
0.15643447	81°	9π20
0.1391731	82°	41π90
0.12186934	83°	83π180
0.10452846	84°	7π15
0.08715574	85°	17π36
0.06975647	86°	43π90
0.05233596	87°	29π60
0.0348995	88°	22π45
0.01745241	89°	89π180
0	90°	π2
-0.01745241	91°	91π180
-0.0348995	92°	23π45
-0.05233596	93°	31π60
-0.06975647	94°	47π90
-0.08715574	95°	19π36
-0.10452846	96°	8π15
-0.12186934	97°	97π180
-0.1391731	98°	49π90
-0.15643447	99°	11π20
-0.17364818	100°	5π9
-0.190809	101°	101π180
-0.20791169	102°	17π30
-0.22495105	103°	103π180
-0.2419219	104°	26π45
-0.25881905	105°	7π12
-0.27563736	106°	53π90
-0.2923717	107°	107π180
-0.30901699	108°	3π5
-0.32556815	109°	109π180
-0.34202014	110°	11π18
-0.35836795	111°	37π60
-0.37460659	112°	28π45
-0.39073113	113°	113π180
-0.40673664	114°	19π30
-0.42261826	115°	23π36
-0.43837115	116°	29π45
-0.4539905	117°	13π20
-0.46947156	118°	59π90
-0.48480962	119°	119π180
-0.5	120°	2π3
-0.51503807	121°	121π180
-0.52991926	122°	61π90
-0.54463904	123°	41π60
-0.5591929	124°	31π45
-0.57357644	125°	25π36
-0.58778525	126°	7π10
-0.60181502	127°	127π180
-0.61566148	128°	32π45
-0.62932039	129°	43π60
-0.64278761	130°	13π18
-0.65605903	131°	131π180
-0.66913061	132°	11π15
-0.68199836	133°	133π180
-0.69465837	134°	67π90
-0.70710678	135°	3π4
-0.7193398	136°	34π45
-0.7313537	137°	137π180
-0.74314483	138°	23π30
-0.75470958	139°	139π180
-0.76604444	140°	7π9
-0.77714596	141°	47π60
-0.78801075	142°	71π90
-0.79863551	143°	143π180
-0.80901699	144°	4π5
-0.81915204	145°	29π36
-0.82903757	146°	73π90
-0.83867057	147°	49π60
-0.8480481	148°	37π45
-0.8571673	149°	149π180
-0.8660254	150°	5π6
-0.87461971	151°	151π180
-0.88294759	152°	38π45
-0.89100652	153°	17π20
-0.89879405	154°	77π90
-0.90630779	155°	31π36
-0.91354546	156°	13π15
-0.92050485	157°	157π180
-0.92718385	158°	79π90
-0.93358043	159°	53π60
-0.93969262	160°	8π9
-0.94551858	161°	161π180
-0.95105652	162°	9π10
-0.95630476	163°	163π180
-0.9612617	164°	41π45
-0.96592583	165°	11π12
-0.97029573	166°	83π90
-0.97437006	167°	167π180
-0.9781476	168°	14π15
-0.98162718	169°	169π180
-0.98480775	170°	17π18
-0.98768834	171°	19π20
-0.99026807	172°	43π45
-0.99254615	173°	173π180
-0.9945219	174°	29π30
-0.9961947	175°	35π36
-0.99756405	176°	44π45
-0.99862953	177°	59π60
-0.99939083	178°	89π90
-0.9998477	179°	179π180
-1	180°	π

How to use this inverse cosine calculator

The arc cosine calculator is not difficult to use. Enter the cosine value (between -1 and 1) and click Calculate to find the corresponding angle. Angles are expressed in degrees and radians. If you want to recalculate, please click the Reset button first.

FAQS

Q: What is inverse cosine used for?
A: Inverse cosine is used to find the corresponding angle based on the cosine value.

Q: Are arccos and cos^-1 the same?
A: Yes, they are both expressions of arccosine.

Q: Are arccos and secant the same?
A: No. Arccos is the inverse function of cosine, and secant is the reciprocal of cosine.

Q: Is inverse cosine even or odd?
A: Arccosine is neither odd nor even.

Q: Why doesn't inverse cosine work?
A: The main reason arccosine doesn’t work is that the value is outside its domain. The domain of arccosine is between -1 and 1.

Q: What is the arccosine domain and range?
A: The domain of arccosine is [-1, 1]. The range of arccosine is [0, π].

Conclusion

In a right triangle, the arccosine is considered an angle whose measure is given by the trigonometric ratio of its adjacent side to the hypotenuse. It is one of the 6 inverse trigonometric functions (others are arcsine, arctangent, arccotangent, arcsecant and arccosecant). If you want to calculate the arccosine, please use our arccosine calculator, which is very convenient and fast, and the key is free.