Heronian Mean Calculator

Welcome to the Heronian mean calculator which calculates the Heronian mean of two positive numbers.

The Heronian mean is an average of two non-negative real numbers, represented by H, and its formula is

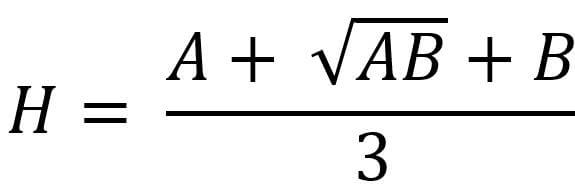The Heronian mean can also be regarded as the weighted mean of the arithmetic mean and the geometric mean. The corresponding weights are 23 and 13. The formula is as follows

1. Calculate the product of two non-negative numbers.

AB

2. Find the square root of a product.

√AB

3. Find the sum of two numbers.

A + B

4. Calculate the Heronian mean

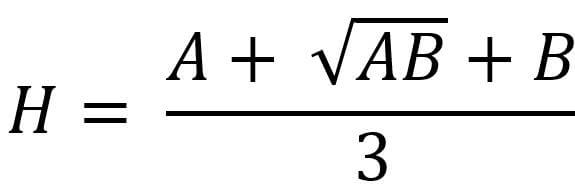
For example, what is the Heronian mean of 3 and 12?

H = 3 + √3*12 + 123 = 213 = 7

Using the calculator is simple, follow these 2 steps:

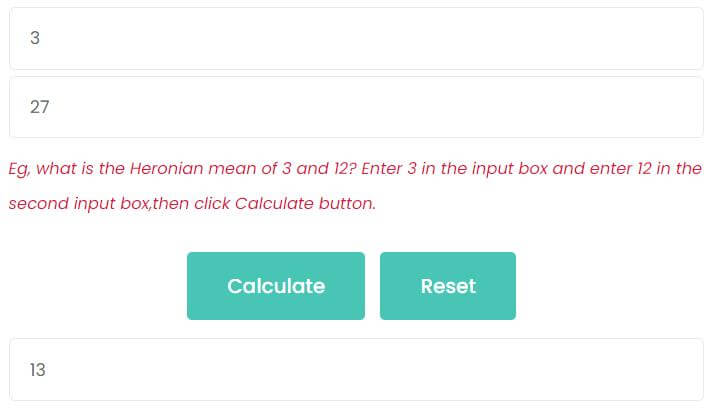
For example, find the Heronian mean of 3 and 27.

Enter 3 in the first input box.

Enter 27 in the second input box.

Then, click Calculate button. As the picture shows, the Heronian mean is 13.