The greatest common divisor calculator is an online tool that easily computes the greatest common divisor of 2 or more integers, or whole numbers, instead of you doing it by hand.
What is the greatest common divisor
First, let’s find out the meaning of greatest common divisor (GCD). The GCD is the biggest number that divides more than 2 numbers without leaving a remainder. It is called by many names – greatest common factor (GCF), highest common divisor (HCD), and highest common factor (HCF). When you come across any one of these names, do not get into a confusion because it all means the same. In this article we will use only the GCF and GCD, to avoid confusion like the lack of certainty while using it.
For example, the GCD of 15 and 20 is 5. 5 divides both these numbers 15 and 20 and no other larger number is able to do the same. The principle is easily stretched out to sets of more than 2 numbers, which can also mean that the GCD of this set of numbers is the largest number that divides each of them.
Factors are numbers that can be multiplied together to get a product or result, like for example, 2 * 3 = 6. The numbers 2 and 3 are factors. A number can have many factors.
factors of 10: 1, 2, 5 and 10.
Common factors are numbers that appear on the list of factors of 2 or more numbers. If it is a factor of 2 or more numbers, it is a common factor.
Factors of 12 and 30
Factors of 12: 1, 2, 3, 4, 6 and 12
Factors of 30: 1, 2, 3, 5, 6, 10, 15 and 30
Since the numbers 1, 2, 3, and 6 appear on both lists, the common factors of 12 and 30 are 1, 2, 3, and 6.
The Greatest Common Factor is the largest or the highest of the common factors. In our example, 6 is the greatest common factor of 12 and 30.
How to use the greatest common divisor
The greatest common divisor or greatest common factor is used for various applications in number theory especially in modular arithmetic or clock arithmetic, as it is sometimes referred to. Modular arithmetic is a way of doing arithmetic with integers, and just like the hours on a clock which repeat every 12 hours, once the numbers reach the modulus (or a certain value), they go back to zero.
The GCD is also used for other applications, both simple and complex. In fact, you might have calculated GCDs, without actually realizing it, when you are trying to simplify a fraction. Simplifying or reducing a fraction is done by dividing the numerator and denominator by their GCD.
How to calculate the greatest common divisor
Because the GCD has become a fundamental concept to number theory, some algorithms were introduced to officially compute it. Here are the 4 types of algorithms used in calculating the GCD or GCF.
1. Prime Factorization Method
This is the method by which numbers are broken down into their prime numbers. A prime number has precisely exactly 2 factors: the number and 1. If both numbers are prime, their GCD is 1. Prime factorization is done in 2 manners.
Division Method
The given number is divided by the prime number, and repeats the process until the resulting quotient is 1. Next is multiplying all prime factors that are divisors.
Factor Tree Method
The given number is written on top of the factor tree, while the corresponding pairs of factors are written as the branches of the tree. Next, the composite factors are factorized again, and written down as the next branches; and so on until we get the prime factors of all the composite factors.
Example of Prime Factorization Method: Find the GCD of 42 and 70.
Step 1: Finding the prime numbers of each of these numbers:
42 = 2 * 3 * 7
70 = 2 * 5 * 7
Step 2: highlight all common factors:
42 = 2 * 3 * 7
70 = 2 * 5 * 7
The common factors are in bold.
The GCD of 42 and 70 is 2 * 7 = 14
2. Repeated Division Method
This method is to divide all numbers by the lowest prime number; and the process is done repeatedly until all numbers can no longer be divided by that number. Next, divide it with the next prime number up to the point that the number is completely factored with all the factors as prime numbers.
Example of Repeated Division Method: Find the GCD of 84 and 140.
Step 1: Write down the 2 numbers
84 140
Step 2: Divide both numbers by 2, again by 2, and by the next prime number 7
The common factors are 2 * 2 * 7 = 28
The GCD of 84 and 140 is 28.
3. Euclidean Algorithm Method
This is a way of finding the greatest common divisor of 2 numbers by dividing the larger number by the smaller, the smaller by the remainder, the first remainder by the second remainder, until the exact divisor is obtained, and this is the GCD.
Example of Euclidean Algorithm Method: Find the GCD of 36 and 52.
Step 1: Divide 52 by 36. The answer is 1 with a remainder 16.
Step 2: Divide 36 by the remainder 16 = 32 with remainder 4
Step 3: Divide 16 by the remainder 4 = 4 with remainder 0
The GCD of 52 and 36 is 4.
4. Listing Out All The Factors Method
This involves writing all the factors of each number and then identifying the common factors. Highlight the common factors so that the difference can be made out. After all the common factors have been identified, select the number which has the largest value, and this will, essentially be the GCD.
Example 1 of Listing Method: Find GCD of 12 and 18.
Step 1: find all the divisors of the above numbers 18 and 12.
Divisors of 12: 1, 2, 3, 4, 6, 12
Divisors of 18: 1, 2, 3, 6, 9, 18
Step 2: the greatest common factor: 6.
Most often, in Math, as the numbers increase, there is also an increase in the level of difficulty of problem solving. This applies also in finding the GCD of 2 large numbers, but the procedure does not change. Here’s another example of listing method using larger numbers.
Example 2 of Listing Method: Find the GCD of 64 and 96.
Step 1: Find the common factors of the given numbers.
Factors of 64: 1, 2, 4, 8, 16, 32, 64
Factors of 96: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96
Step 2: Compare the listed factors. There are 6 common factors, namely, 1, 2, 4, 8, 16 and 32. The one with the biggest value is 32, and hence is the GCD of the given numbers.
The above methods of finding the GCD are practical to do manually. However, it may take more time and in cases of large numbers, the process can be long and difficult. A better approach is to use the greatest common divisor (GCD) calculator. It takes only a few seconds or less to find the GCD of any given numbers, big or small.
How to use the GCD calculator
Using the GCD Calculator is a simple and easy process. Just follow the following steps.
- Enter the values on the input box, using a comma to separate each values.
- Press the “Calculate” button, you will get the greatest common divisor of the given numbers.
- Press the “Reset” button to get ready for another calculation.
When doing a manual calculation, you will notice that the methods are a bit complicated and thus confusing. So why insist on doing it when you can easily get results by simply using the GCD calculator. Experience the ease of using this calculator, as it is simple and hassle free to use, and you can add it on your online platforms.
Next, let’s take a few examples to see how this calculator is used.
Solved examples using GCD Calculator
Find the GCD of 2 numbers
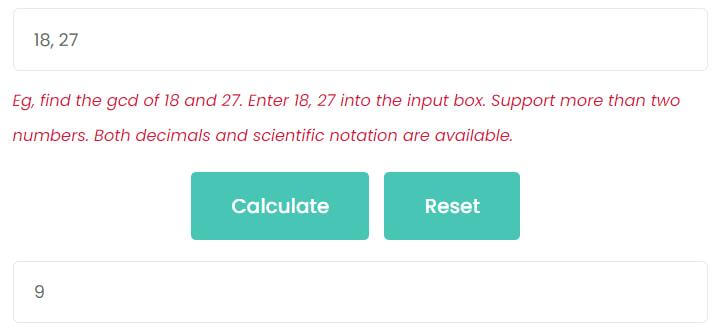
For example, find the GCD of 18 and 27.
Enter 18, 27 on the input box, then click Calculate button. As the picture shows, the greatest common divisor of 18 and 27 is 9.
Find the GCD of 3 numbers
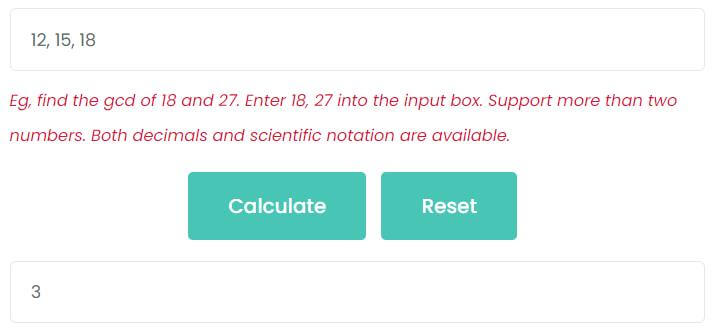
For example, find the GCD of 12, 15 and 18.
Enter 12, 15, 18 on the input box, then click Calculate button. As the picture shows, the greatest common divisor of 12, 15 and 18 is 3.
Find the GCD of 4 or more numbers
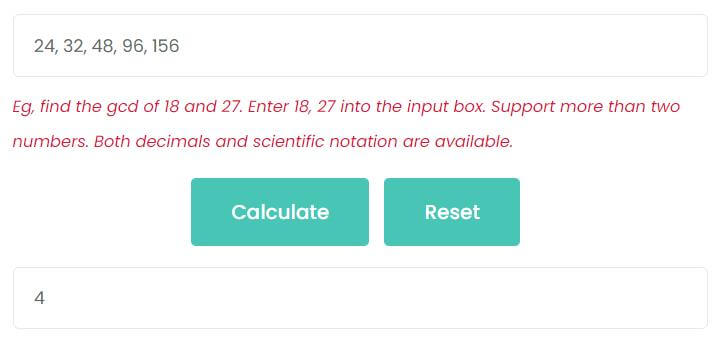
For example, find the GCD of 24, 32, 48, 96 and 156.
Enter 24, 32, 48, 96, 156 on the input box, then click Calculate button. As the picture shows, the greatest common divisor of 24, 32, 48, 96 and 156 is 4.
Latest calculators
Standard Form to Slope-Intercept Form Calculator
Slope Intercept Form Calculator
Slope Calculator: Calculate Slope, X-Intercept, Y-Intercept
Reciprocal of Complex Number Calculator
Conjugate Complex Number Calculator
Modulus of Complex Number Calculator
Profit Percentage Calculator: Calculate Your Profitability Easily
Attendance and Absence Percentage Calculator
Circular Segment Radius Calculator
Regular Polygon Side Length Calculator
Annulus Calculator for Width, Perimeter, and Area