Welcome to use the fraction to decimal calculator, where you can easily convert fractions to decimals. Fractions support improper fractions and mixed fractions.
What are fractions and decimals?
Fraction refers to the fraction of a number to another number, or the ratio of an event to all events. Divide the unit 1 into several equal parts, which means that the number of such one or several parts is called a fraction. There are 3 types of fractions: proper fraction, improper fraction and mixed fraction. The numerator at the top and the denominator at the bottom. You can also think of it as a division, divide the numerator by the denominator to get a decimal.
Decimal is a special form of real number, usually composed of 3 parts: integer part, decimal point and decimal part. The decimal point is in the middle of integer and decimal. Decimals can be expressed as fractions.
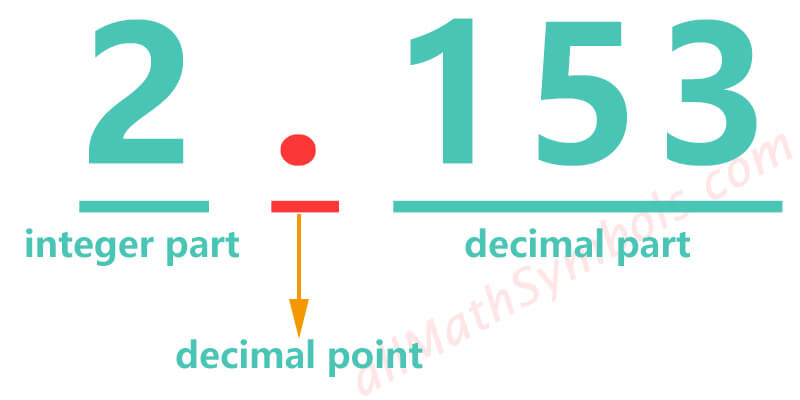
How to convert fractions to decimals?
Through the above introduction, we know the concept of fractions and decimals. To convert a fraction into a decimal, you can directly divide the numerator by the denominator. Therefore, the key point is the division calculation, as long as you understand the usage of division, you can easily convert the fraction to a decimal. Maybe it is easy to divide a small number, but it is relatively difficult to divide a large number. So, we developed this free online fraction to decimal calculator to help you quickly complete the conversion.
How to use the fraction to decimal calculator?
When we design the fraction to decimal calculator, in addition to the numerator and denominator, we also reserve a whole number input box. It is to support the conversion of mixed fractions to decimals. Therefore, in the process of using, when we encounter mixed fractions, enter the integer part into the whole number input box. For common fractions and improper fractions, just enter the numerator and denominator. Then, click the calculate button. The answer will appear in the blink of an eye, with 8 decimal places by default. Here are some examples to show how the fraction to decimal calculator is used.
Solved examples using fraction to decimal calculator
Common fractions to decimals
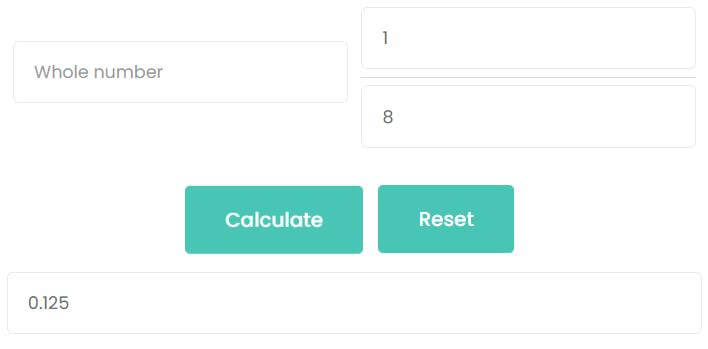
For example, What is 18 as a decimal?
Enter 1 into the numerator input box, enter 8 into the denominator input box. Then click calculate button. As the picture shows, the decimal of 18 is 0.125.
Improper fractions to decimals
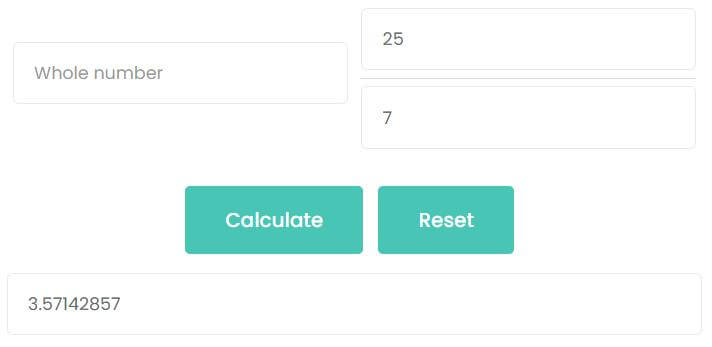
For example, What is 257 as a decimal?
Enter 25 into the numerator input box, enter 7 into the denominator input box. Then click calculate button. As the picture shows, the decimal of 257 is 3.57142857.
Mixed fractions to decimals
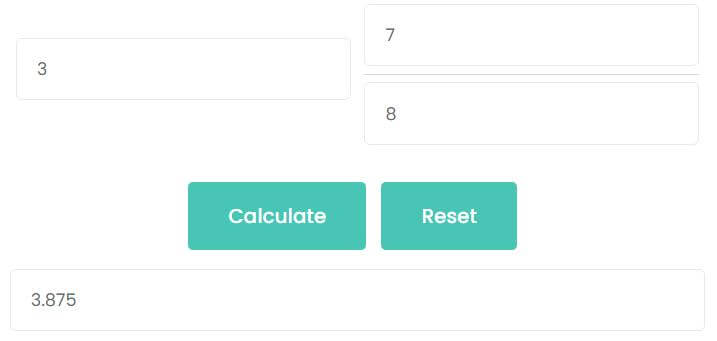
For example, What is 3 and 78 as a decimal?
First, enter 3 into the whole number input box. Then, enter 7 into the numerator input box, enter 8 into the denominator input box. Then click calculate button. As the picture shows, the decimal of 378 is 3.875.
Latest calculators
Standard Form to Slope-Intercept Form Calculator
Slope Intercept Form Calculator
Slope Calculator: Calculate Slope, X-Intercept, Y-Intercept
Reciprocal of Complex Number Calculator
Conjugate Complex Number Calculator
Modulus of Complex Number Calculator
Profit Percentage Calculator: Calculate Your Profitability Easily
Attendance and Absence Percentage Calculator
Circular Segment Radius Calculator
Regular Polygon Side Length Calculator
Annulus Calculator for Width, Perimeter, and Area