Welcome to the free online calculator to find two numbers by given geometric and arithmetic mean. For example, the geometric mean of two numbers is 20, and their arithmetic mean is 25. What are the two numbers?
Find 2 Numbers by Geometric and Arithmetic Mean Calculator
The geometric mean of two numbers is a, and their arithmetic mean is b. What are the two numbers?
Eg, the geometric mean of two numbers is 20, and their arithmetic mean is 25. What are the two numbers? Enter 20 in the first input box and enter 25 in the second input box. Then click Calculate button.
What is the geometric mean?
The geometric mean corresponds to the central tendency of a set of numbers using the product of the values, and it contrasts with the arithmetic mean, which uses the sum of values. So, the geometric mean is computed as the Nth root of the product of n numbers. A geometric mean is only calculated for positive integers. The formula for the geometric mean is
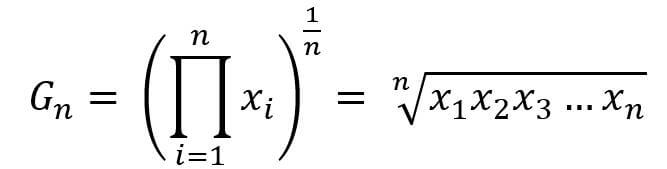
What is the arithmetic mean?
The arithmetic mean, also known as the average, refers to the sum of a set of numbers divided by the total number of numbers in the set.
The arithmetic mean formula is
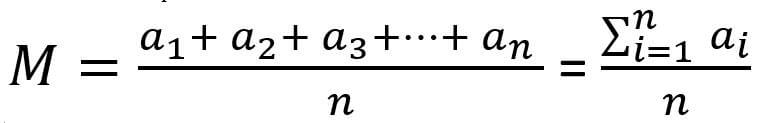
How to find two numbers based on the given geometric and arithmetic mean
Next, use the example at the beginning of the article to explain how to find two numbers based on the given geometric and arithmetic mean.
The geometric mean of two numbers is 20, and their arithmetic mean is 25. What are the two numbers?
Let the two numbers be x and y.
So, we can list the geometric mean and the average of these two numbers.
√xy = 20………(1)
x + y2 = 25………(2)
Square both sides of equation 1 at the same time.
√xy = 20
xy = 400………(3)
Simplify the second equation.
x + y2 = 25
x + y = 50………(4)
Now the problem becomes that the sum of two numbers is 50 and the product of the two numbers is 400, find the two numbers. It can be solved with find two numbers by sum and product calculator.
Continue to solve.
Simplify the 4th equation, let x be represented by y.
x + y = 50
x = 50 – y………(5)
Substitute x = 50 – y into the third equation and simplify.
xy = 400
(50 – y) y = 400
50y – y2 = 400
y2 – 50y + 400 = 0
(y – 10) (y – 40) = 0
y = 10 or y = 40
According to the relationship between x and y, we can calculate the value of x.
x = 50 – y = 50 – 10 = 40
or
x = 50 – y = 50 – 40 = 10
So, the two numbers are 10 and 40.
Verify.
√10 * 40 = √400 = 20
10 + 402 = 502 = 25
Correct.
How to use the calculator to find two numbers by given geometric and arithmetic mean
Using the calculator is simple, follow these 3 steps:
- Enter the geometric mean in the first input box.
- Enter the arithmetic mean in the second input box.
- Click Calculate button to get the answer, or click Reset button to start a new calculation.
Next, let’s look at some examples.
Solved examples using the calculator
Example 1: The geometric mean of two numbers is 8 and their arithmetic mean is 17, find the two number.
Enter 8 in the first input box.
Enter 17 in the second input box.
Then click Calculate button, as shown in the figure, the two numbers are 2 and 32.
√2 * 32 = √64 = 8
2 + 322 = 342 = 17

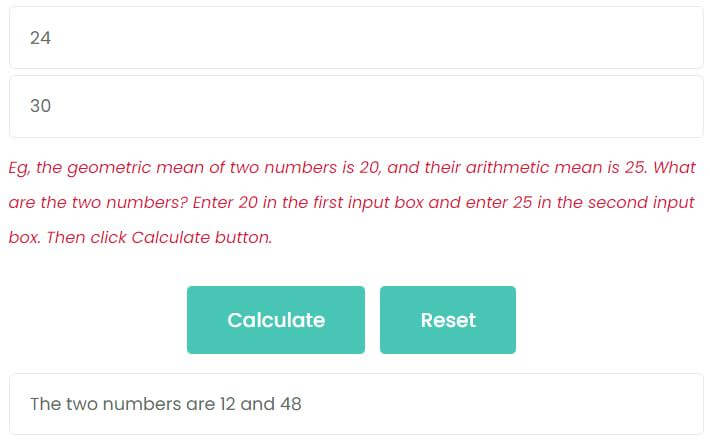
Example 2: The geometric mean of two numbers is 24 and their arithmetic mean is 30. What are the numbers?
Enter 24 in the first input box.
Enter 30 in the second input box.
Then click Calculate button, as shown in the figure, the two numbers are 12 and 48.
√12 * 48 = √576 = 24
12 + 482 = 602 = 30
Latest Calculators
Standard Form to Slope-Intercept Form Calculator
Slope Intercept Form Calculator
Slope Calculator: Calculate Slope, X-Intercept, Y-Intercept
Reciprocal of Complex Number Calculator
Conjugate Complex Number Calculator
Modulus of Complex Number Calculator
Profit Percentage Calculator: Calculate Your Profitability Easily
Attendance and Absence Percentage Calculator
Circular Segment Radius Calculator
Regular Polygon Side Length Calculator
Annulus Calculator for Width, Perimeter, and Area