Welcome to the free online calculator to find two numbers by given difference and LCM. For example, the difference of two numbers is 14 and their LCM is 441. What are the numbers?
How to find two numbers based on the given difference and LCM
LCM stands for least common multiple, which refers to the smallest positive integer that is divisible by 2 numbers. It is called by many names – Lowest Common Multiple (LCM), Smallest Common Divisor (SCD), Lowest Common Denominator (LCD) and Least Common Factor (LCF).
Now, how to solve the problem mentioned above?
There are 3 methods. In the following, a detailed description will be given in conjunction with the above example.
Method 1: Common Method
Let the numbers be x and y.
Since their LCM is 441, we can get two equations
ax = 441………(1)
by = 441………(2)
Here, a and b are both integers and coprime.
Therefore, we can get the values of x and y.
x = 441a………(3)
y = 441b………(4)
The difference of them is 14.
x – y = 14………(5)
Substitute the third and fourth equations into the 5th equation and simplify.
x – y = 14
441a – 441b = 14
1a – 1b = 14441
b – aab = 14441………(6)
Did you find anything? Yes, there are fractions on the left and right sides of this equation. Therefore, the equation can be split into two equations: the left and right numerators and denominators are equal respectively.
b – a = 14………(7)
ab = 441………(8)
Now, the question becomes that the difference of two numbers is 14 and their product is 441. What are the numbers? How to solve it? There are 2 methods, one is the quadratic equation method and the other is the factor method. For the specific process, please refer to the calculator finds two numbers by difference and product.
Here, the quadratic equation method is used to solve.
Since b – a = 14, so b = 14 + a. Put this value into the 8th equation.
ab = 441
a(14 + a) = 441
a2 + 14a = 441
a2 + 14a – 441= 0
(a – 49) (a + 63) = 0
a = 49 or a = -63
From the relationship between a and b, we can easily calculate the value of b.
b = 14 + a = 14 + 49 = 63
or
b = 14 + a = 14 + (-63) = -49
Note that these are the values of a and b, not the x and y we assume.
According to Equation 3 and Equation 4, the values of x and y can be calculated.
When a = 49 and b = 63
x = 441a = 44149 = 9
y = 441b = 44163 = 7
When a = -63 and b = -49
x = 441a = 441-63 = -7
y = 441b = 441-49 = -9
Now, we get the two numbers are (9, 7) or (-7, -9).
Verify.
9 – 7 = 2
Incorrect.
A difference of 7 times from 14. So, scale them up by a factor of 7, the two numbers are (63, 49) or (-49, -63).
Let’s check again.
63 – 49 = 14
LCM(63, 49) = 441
Or
(-49) – (-63) = 14
LCM(-49, -63) = 441
Correct now.
Method 2: HCF Method
Here, we do not directly assume these two numbers but assume that the highest common factor of these two numbers is a. Therefore, we can get these two numbers as ax and ay, where x and y are relatively prime.
ax – ay = 14………(1)
Since the product of two numbers is equal to the product of the LCM and HCF of the two numbers, we can get the equation.
ax * ay = LCM(ax, ay) * HCF(ax, ay)
a2xy = 441 * a
axy = 441………(2)
Divide Equation 1 by Equation 2
ax – ayaxy = 14441
x – yxy = 14441
Does it look familiar? Yes, go back to the same steps as method one. Ignore the remaining steps and go straight to the third method.
Method 3: Factor Method
Since the LCM of two numbers is 441, the two numbers must be factors of 441. So, we can calculate the factors of 441 first. Then, find the two numbers in the factors that subtract to 14.
With the find all factors calculator, we can easily get the factors of 441 are
1, 3, 7, 9, 21, 49, 63, 147, 441
Among them, there are 2 pairs of two numbers whose difference is 14.
21 – 7 = 14
63 – 49 = 14
The LCM of 7 and 12 is 84. Ineligible.
So, the answer is also 49 and 63.
Well, these are three common solutions that, each of which is not a simple process. So, we developed this free calculator to find two numbers by given difference and LCM. No calculations required and displays the answer in milliseconds.
Next, we will introduce how to use the calculator.
How to use the calculator to find two numbers by difference and LCM
Using the calculator is simple, follow these 3 steps:
- Enter the difference in the first input box.
- Enter the LCM in the second input box.
- Click Calculate button to get the answer, or click Reset button to start a new calculation.
Next, let’s look at some examples.
Solved examples using the calculator to find two numbers by difference and LCM
Example 1: The difference of two numbers is 10 and their LCM is 495. What are the numbers?
Enter 10 in the first input box.
Enter 495 in the second input box.
Then click Calculate button, as shown in the figure, the two numbers are 45 and 55.
55 – 45 = 10
LCM(45, 55) = 495

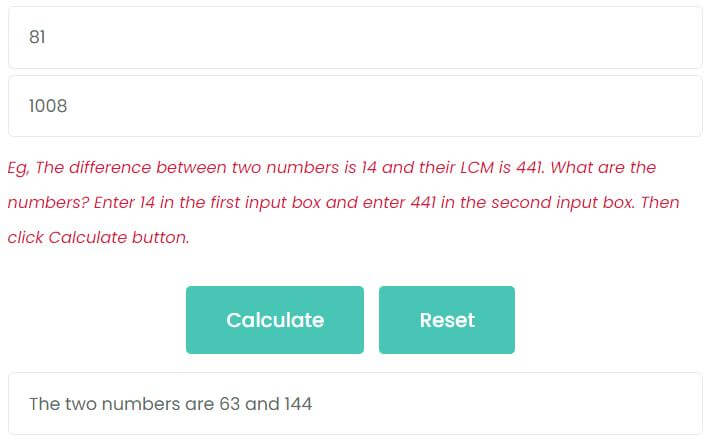
Example 2: The difference of two numbers is 81 and their LCM is 1008. What are the numbers?
Enter 81 in the first input box.
Enter 1008 in the second input box.
Then click Calculate button, as shown in the figure, the two numbers are 63 and 144.
144 – 63 = 81
LCM(144, 63) = 1008
Latest Calculators
Standard Form to Slope-Intercept Form Calculator
Slope Intercept Form Calculator
Slope Calculator: Calculate Slope, X-Intercept, Y-Intercept
Reciprocal of Complex Number Calculator
Conjugate Complex Number Calculator
Modulus of Complex Number Calculator
Profit Percentage Calculator: Calculate Your Profitability Easily
Attendance and Absence Percentage Calculator
Circular Segment Radius Calculator
Regular Polygon Side Length Calculator
Annulus Calculator for Width, Perimeter, and Area