Are you looking for a simple and efficient way to calculate coversine? Look no further! In this article, we’ll introduce you to the coversine function, explain its definition and formula, and guide you through the process of using the Coversine Calculator. Whether you’re a student, a professional, or simply curious about trigonometry, this calculator will help you accurately determine the coversine of any angle. Let’s dive in!
What is Coversine
Coversine is a trigonometric function closely related to the sine function. It is defined as the complement of the sine function. The formula to calculate coversine is straightforward:
Coversine(x) = 1 – sine(x)
In terms of the unit circle, the coversine is the distance between the point on the circle and the x-axis. As the angle increases, the coversine value decreases, reaching its minimum value of 0 when the angle is 90 degrees or π2 radians.
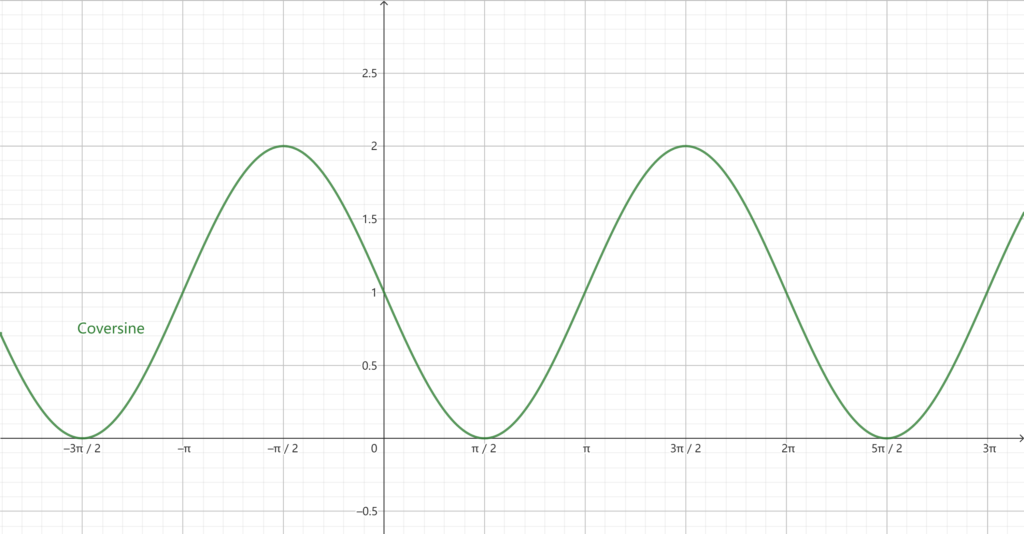
Coversine Graph
For example, let’s calculate the coversine of an angle of 60 degrees manually.
Step 1: Calculate the sine of the angle.
We can use the sine calculator or reference tables to find that the sine of 60 degrees is
sine(60°) = √32
Step 2: Calculate the coversine value.
The coversine is defined as the complement of the sine function. So, we can calculate the coversine by sine value.
coversine(60°) = 1 – sine(60°) = 1 – √32 = 2 – √32
After performing the calculations, we find that the coversine of 60 degrees is 2 – √32.
By following these steps, you can manually calculate the coversine of any angle. However, using a calculator or specialized tool like the Coversine Calculator can provide more accurate and efficient results.
Coversine Table
| Degrees | Radians | Coversine |
| 0° | 0 | 1 |
| 5° | π36 | 0.91284426 |
| 10° | π18 | 0.82635182 |
| 15° | π12 | 0.74118095 |
| 20° | π9 | 0.65797986 |
| 25° | 5π36 | 0.57738174 |
| 30° | π6 | 0.5 |
| 35° | 7π36 | 0.42642356 |
| 40° | 2π9 | 0.35721239 |
| 45° | π4 | 0.29289322 |
| 50° | 5π18 | 0.23395556 |
| 55° | 11π36 | 0.18084796 |
| 60° | π3 | 0.1339746 |
| 65° | 13π36 | 0.09369221 |
| 70° | 7π18 | 0.06030738 |
| 75° | 5π12 | 0.03407417 |
| 80° | 4π9 | 0.01519225 |
| 85° | 17π36 | 0.0038053 |
| 90° | π2 | 0 |
| 95° | 19π36 | 0.0038053 |
| 100° | 5π9 | 0.01519225 |
| 105° | 7π12 | 0.03407417 |
| 110° | 11π18 | 0.06030738 |
| 115° | 23π36 | 0.09369221 |
| 120° | 2π3 | 0.1339746 |
| 125° | 25π36 | 0.18084796 |
| 130° | 13π18 | 0.23395556 |
| 135° | 3π4 | 0.29289322 |
| 140° | 7π9 | 0.35721239 |
| 145° | 29π36 | 0.42642356 |
| 150° | 5π6 | 0.5 |
| 155° | 31π36 | 0.57738174 |
| 160° | 8π9 | 0.65797986 |
| 165° | 11π12 | 0.74118095 |
| 170° | 17π18 | 0.82635182 |
| 175° | 35π36 | 0.91284426 |
| 180° | π | 1 |
| 185° | 37π36 | 1.08715574 |
| 190° | 19π18 | 1.17364818 |
| 195° | 13π12 | 1.25881905 |
| 200° | 10π9 | 1.34202014 |
| 205° | 41π36 | 1.42261826 |
| 210° | 7π6 | 1.5 |
| 215° | 43π36 | 1.57357644 |
| 220° | 11π9 | 1.64278761 |
| 225° | 5π4 | 1.70710678 |
| 230° | 23π18 | 1.76604444 |
| 235° | 47π36 | 1.81915204 |
| 240° | 4π3 | 1.8660254 |
| 245° | 49π36 | 1.90630779 |
| 250° | 25π18 | 1.93969262 |
| 255° | 17π12 | 1.96592583 |
| 260° | 13π9 | 1.98480775 |
| 265° | 53π36 | 1.9961947 |
| 270° | 3π2 | 2 |
| 275° | 55π36 | 1.9961947 |
| 280° | 14π9 | 1.98480775 |
| 285° | 19π12 | 1.96592583 |
| 290° | 29π18 | 1.93969262 |
| 295° | 59π36 | 1.90630779 |
| 300° | 5π3 | 1.8660254 |
| 305° | 61π36 | 1.81915204 |
| 310° | 31π18 | 1.76604444 |
| 315° | 7π4 | 1.70710678 |
| 320° | 16π9 | 1.64278761 |
| 325° | 65π36 | 1.57357644 |
| 330° | 11π6 | 1.5 |
| 335° | 67π36 | 1.42261826 |
| 340° | 17π9 | 1.34202014 |
| 345° | 23π12 | 1.25881905 |
| 350° | 35π18 | 1.17364818 |
| 355° | 71π36 | 1.08715574 |
| 360° | 2π | 1 |
What is Coversine Calculator
The Coversine Calculator is a powerful tool designed to simplify the process of calculating coversine. Its purpose is to provide quick and accurate results, saving you time and effort in manual calculations. With the Coversine Calculator, you can easily obtain the coversine value for any given angle without the need for complex mathematical operations.
How to Use the Coversine Calculator
Using the Coversine Calculator is a straightforward process. Here’s a step-by-step guide:
- Enter the desired angle value in the input box.
- Select the angle type, degrees or radians, the default is degrees.
- Click the Calculate button to obtain the coversine value.
- Click the Reset button to start a new calculation
FAQs
- Q: What is the relationship between coversine and sine?Coversine is the complement of the sine function, obtained by subtracting the sine value from 1.
- Q: Can coversine values be negative?A: No, coversine values are always non-negative, ranging from 0 to 2. (You can get the answer from Coversine Graph above.)
- Q: Is there a direct formula to calculate the coversine?
- Q: Can the coversine be greater than 1?A: Yes, The coversine function ranges between 0-2.
- Q: In which fields is coversine commonly used?A: Coversine has applications in various fields such as mathematics, physics, engineering, and computer graphics, particularly when dealing with angles and trigonometric calculations.
Conclusion
The Coversine Calculator is a valuable tool that simplifies the process of calculating coversine. Whether you’re a student studying trigonometry or a professional requiring precise angle measurements, this calculator will provide you with accurate coversine values instantly. Embrace the convenience and efficiency of the Coversine Calculator to enhance your trigonometric calculations and gain a deeper understanding of angles and their components.
Latest Calculators
Standard Form to Slope-Intercept Form Calculator
Slope Intercept Form Calculator
Slope Calculator: Calculate Slope, X-Intercept, Y-Intercept
Reciprocal of Complex Number Calculator
Conjugate Complex Number Calculator
Modulus of Complex Number Calculator
Profit Percentage Calculator: Calculate Your Profitability Easily
Attendance and Absence Percentage Calculator
Trigonometric Functions
Arccsc Calculator – Find the Exact Value of Inverse Cosecant
Arcsec Calculator – Find the Exact Value of Inverse Secant
Arccot Calculator – Find the Exact Value of Inverse Cotangent
Arctan Calculator – Find the Exact Value of Inverse Tangent
Inverse Cosine Calculator – Find The Exact Value of Arccos
Inverse Sine Calculator – Find The Exact Value of Arcsin
Inverse Trigonometric Functions Calculator
Trigonometric Functions Conversion Calculator
Trig Calculator – Find 6 Trigonometric Functions by Angles or Sides